RAZONES TRIGONOMETRICAS INVERSAS RESUELTAS

Las expresiones arcsen, arccos y arctan son las abreviaturas de arco seno, arco coseno y arco tangente, respectivamente. 

Los operadores trigonométricos inversos se utilizan para definir las reglas de correspondencia de las funciones trigonométricas inversas, de allí que van a cumplir ciertas condiciones para que se puedan utilizar

• CLIC AQUÍ Ver TEORÍA Y EJERCICIOS RESUELTOS PDF
• Ver DOMINIO Y RANGO DE UNA FUNCIÓN TRIGONOMÉTRICA INVERSA
• Ver GRÁFICAS DE LAS FUNCIONES TRIGONOMÉTRICAS INVERSAS
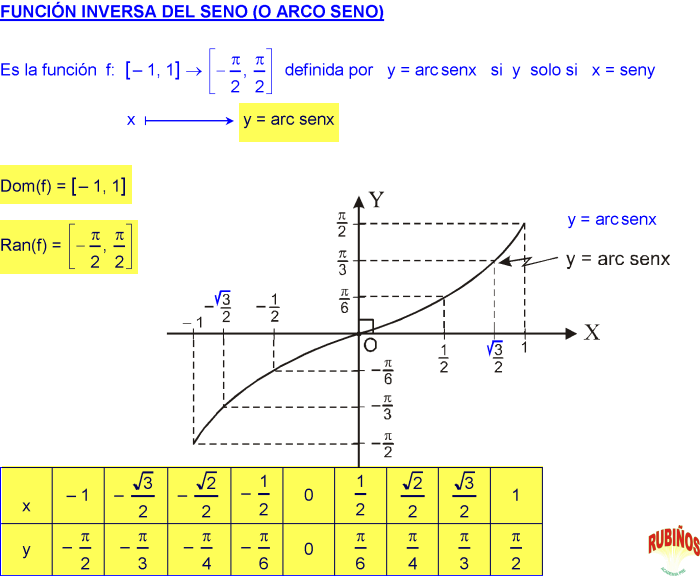
• Ver FUNCIÓN ARCO SENO
• Ver FUNCIÓN ARCO COSENO
• Ver FUNCIÓN ARCO TANGENTE
• Ver FUNCIÓN ARCO COTANGENTE
• Ver FUNCIÓN ARCO SECANTE
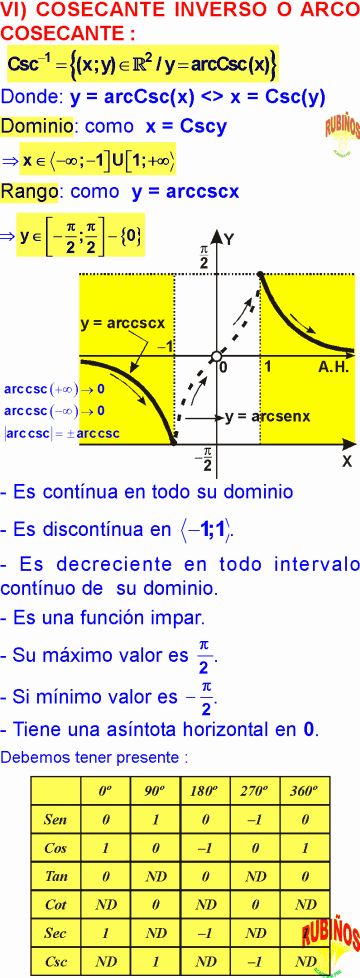
• Ver FUNCIÓN ARCO COSECANTE

*

*

1. Calcule el dominio de la función definida por f ; D) [ –1; 0] E) [ –1; 1〉 2. Definida la función f mediante la regla de correspondencia y f x x x = = ( − ) ( ) ( − ) 4 1 2 1 arcsen arccos determine el dominio de f y dé por respuesta el número de valores enteros del dominio de f. A) 1 B) 2 C) 3 D) 4 E) 5 3. Halle el conjunto solución de la ecuación 2arcsen(3x) = arccos(7x2 ) A) 4/5 B) 2/3 C) 1/5 D) 2/5 E) 3/5 4. Calcule el valor de la expresión 9 2 1 5 cos2  arctan 5      + A) 15 B) 13 C) 11 D) 10 E) 9 5. Calcule el valor de 2 1 5 5 12 5 arctan arctan arccot + A) 2 B) 3 C) 4 D) 1 2 E) 1 4 6. Calcule el valor de sen arctan cos arctan 2 1 3 2 A) 3 4 B) 1 C) 4 3 D) 2 3 E) 3 2 7. Halle el área de la región sombreada. A) 4p u2 B) 5p u2 C) 6p u2 D) 8p u2 E) 9p u2 Y X f(x)=3 π2 x –1 3 arcsen + 8. Determine el rango de la función f definida por f x arccos sen + 6 9. Calcule el rango de la función 12. Determine el valor de la siguiente expresión. tan sen tan sen   4 1 2 2 5 4 1 2 2 5 arc arc A) 5 21 B) 10 21 C) −5 21 D) −10 21 E) 6 21 13. Dada la función f, definida por f x (x) x = arccos 1 1 halle el rango de f.