RAZONES TRIGONOMÉTRICAS EN POSICIÓN STANDAR PROBLEMAS RESUELTOS PDF
OBJETIVOS
☛ Determinar las Razones trigonométricas de un ángulo a partir de una razón trigonométrica dada.
☛ Determinar el signo y el cuadrante de las expresiones trigonométricas.
☛ Definir a los ángulos cuadrantales y sus características.
☛ Determinar las razones trigonométricas de un ángulo cuadrantal.
☛ Aplicar los conceptos del ángulo cuadrantal y del cálculo de sus razones trigonométricas a la resolución de problemas, en particular problemas tipo examen de admisión.
☛ Resolución de problemas, en particular problemas tipo examen de admisión.
ÁNGULO EN POSICIÓN NORMAL
Es un ángulo trigonométrico cuyo vértice es el origen de coordenadas, cuyo lado inicial (L.I.) coincide con el semieje de las abscisas y cuyo lado final (L.F.) nos indica el cuadrante al cual pertenece. También se le denomina ángulo en posición estándar o en posición canónica
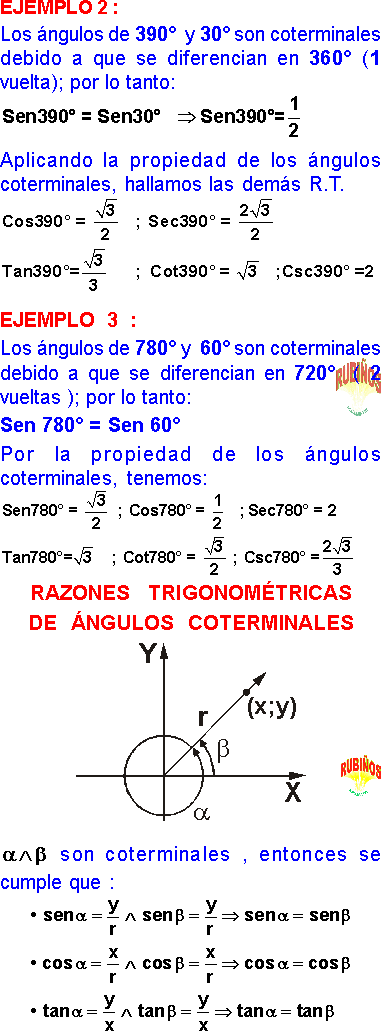
ÁNGULOS COTERMINALES
Son ángulos en posición normal que tienen el mismo lado final.
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO ESTÁNDAR CUALQUIERA
Se define razón trigonométrica de un ángulo estándar a la relación o cociente que se establece entre la abscisa (x), ordenada (y) y radio vector (r) de un punto que pertenece al lado final del ángulo.
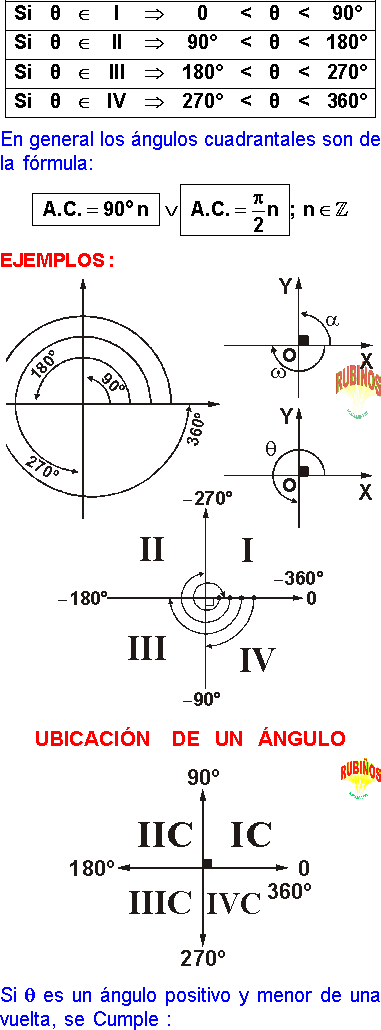
ÁNGULO CUADRANTALES
Son aquellos ángulos en posición normal, cuyo lado final coincide con cualquier de los 4 semiejes coordenados.
Los ángulos cuadrantales no pertenecen a ningún cuadrante.
ÁNGULO CUADRANTAL
Es aquel ángulo en posición normal, cuyo lado final se encuentra en un semieje del plano cartesiano.
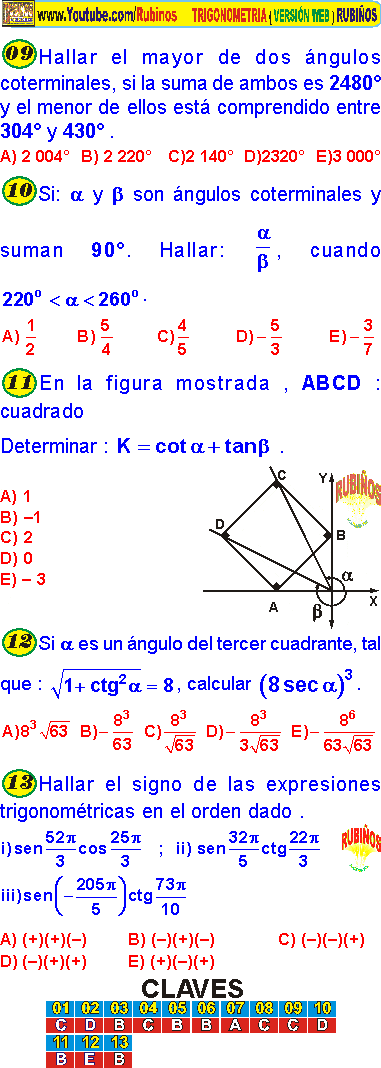
1. De la figura: 3 O x y 7 Calcular el valor de la expresión: W = 4Cos α – 7 Cot α a) –1 b) 0 c) 1 d) 4+ 7 e) 2 7 2. De la figura mostrada: P(x; 4) x y 17 Halle el valor de: H = Tg θ + Cot θ a) 1/4 b) 4 c) 17/4 d) 4/17 e) 21 3. Si el lado final del ángulo en posición estándar "α" pasa por el punto Q(-12;5), calcule el valor de la expresión: M = Csc α – Cot α a) 0 b) 5/12 c) 5 d) 12/5 e) 1/5 4. Si: Cos θ = –0,25; además θ ∈ IIC. Calcular: P = Sec θ – 15 · Tg θ a) 4 b) 7 c) 9 d) 11 e) 19 5. Dada las proposiciones: I. Tg α > 0 ^ Cos α < 0 II. Sen β < 0 ^ Cot β < 0 ¿A qué cuadrantes pertenecen "α“ y "β“ respectivamente? a) I; II b) II; I c) II; III d) III, II e) III; IV 6. Indique el signo de las expresiones: P = Sen 100° + Cos2200° - Tg3300° Q = Tg100 (Sen200 Cot300 ) Cos300 ° ° + ° ° a) +; +; + b) –; +; + c) +; –; – d) –; –; + e) +; +; – 7. Halle el valor de la expresión: M = Sen0 Cos180 Sec360 Sen90 Cot270 ° − ° + ° ° − ° a) –1 b) 0 c) 1 d) 2 e) -2 8. Del gráfico mostrado: 120° O G θ B C A x y Halle “Tg θ“ ; Si: OA=AB=BC; además "G" es baricentro. a) 3 3 b) 3 2 c) 3 d)2 3 e) 3 9 − 9. Si: 225Tg2α–64 = 0; α ∈ IVC. Calcule el valor de la expresión: A = 17Cos α + 15Tg α a) 18 b) 15 c) 11 d) 10 e) 7 10. De la figura mostrada, halle: Tg θ -13 -9 Oθ x y a) 1 3 b) 2 3 c) 1 d) 3 2 e) 3 11. Calcular: Tg θ 1 2 x y a) -2 b) 1 c) -1 d) 1/2 e) 2 12. Si: Tg β = 3 ; |Sen β| = –Sen β Calcular: E = 2 Cos β + Sen β a) 10 2 b) 10 2 − c) 5 2 d) 5 2 − e) 1 2 13. De la figura mostrada: O 60 x y Calcule: A = Cot2α + Csc α a) 1 b) 2 c) 3 d) 4 e) 5 14. Si "α" es un ángulo positivo menor de una vuelta y, β ∈ IIC, además: Sen α + Cos β + |Cos β| = 0 Calcule: Cos α a) 0 b) 1 c) 3 d) –1 e) 3 2 15. De la figura mostrada, halle: Sec α O α (a;a–5) (a+4;1–5a) x y a) 13 2 b)– 13 2 c)– 13 3 d) 13 3 e) 13 16. Si se cumple: 27Sen θ = 91–Sen θ ; θ ∈ IIC Calcule: 21Tg θ a) 2 b) –2 c) 5 d) –5 e) − 21 17. Dado: Csc θ · Sen5θ ·Cos θ < 0 ¿A qué cuadrante pertenece θ? a) IC b) IIC c) IIIC d) IVC e) II ó IIIC 18. Si: P(a; a ), es un punto del lado final de un ángulo en posición estándar “θ". Calcular: 2 A a 1 Sen aSec a a = + ⋅ θ + θ + a) 0 b) 1 c) 2 d) 3 e) –1 ° 19. De la figura mostrada: (-12;0) (0;8) x y O1 Halle: Tg α; O1: Centro a) –1/5 b) –5/12 c) –12/5 d) –13/5 e) –13/12 20. Halle: 3Cot φ, si: Sen Sen Sen ... 3 2 φ + φ + φ + = ; φ ∈ IIC a) − 7 b) 7 2 − c) 3 2 − d) 1 3 − e) 7 3 − CLAVES I 1. b 2. c 3. c 4. d 5. e 6. e 7. d 8. e 9. e 10. b 11. a 12. b 13. e 14. d 15. a 16. b 17. c 18. c 19. e 20. a Problemas II 1. Hallar el valor numérico de la expresión: E = Sen 180°+2Cos 180° +3Sen 270°-5Sec 180°-6Csc270° a) 2 b) 4 c) 6 d) 8 e) 10 2. Indicar los signos de las siguientes expresiones, en el orden F, G, H. 2 3 3 F (Sec285 Tan 138 Sen220 ) Csc 215 Cot338 = ° ⋅ ° ⋅ ° ° ⋅ ° 3 5 4 G (Sen 260 Cos115 Csc116 ) (Csc 195 Tan 336 ) = ° ⋅ ° ⋅ ° ° ⋅ ° 7 H Sen195 Cot340 Csc128 (Tan135 Sec298 ) = ° ⋅ ° ⋅ ° ° ⋅ ° a) –, +, – b) –, –, + c) –, –, – d) + , –, – e) +, +, + 3. De la figura calcular el valor de: E = 5 Csc θ – Cot θ x (-2;1) y a) 1 b) 3 c) 5 d) 7 e) 9 4. De la figura calcular el valor de: P = 13 (Sen α - Cos α) x y (-3;-2) a) -5 b) -3 c) -2 d) 1 e) 2 5. De la figura calcular el valor de: E = (Sen θ + Cos θ)Csc θ x y (7;-24) a) 17/24 b) 24/17 c) 7/24 d) -17/24 e) -7/24 6. Si: Cot α = 2,4 y Sen α < 0; siendo "α" un ángulo en posición estándar. Calcular el valor de: E = 2Sen α + 1 4 Cos α a) –2 b) –1 c) 1/2 d) 1 e) 2 7. Hallar "α+θ". Si cada uno de ellos es ángulo cuadrantal positivo menor que una vuelta y cumplen: Cosα +1 + −1− Cosα = 1− Senθ a) 540° b) 90° c) 180° d) 270° e) 360° 8. Dos ángulos coterminales son proporcionales a los números 5 y 2. Además el mayor de ellos esta comprendido entre 1000° y 1700°. Hallar la suma de dichos ángulos. a) 480° b) 960° c) 1200° d) 1680° e) 1800° 9. Calcular a/b si se tiene que: 2 2 2 (a b) Cos0 2abTan2 4abSec a Sen b Csc 3 2 2 + ° + π + π π + π = 2 a)-3 b) -2 c) –1 d) 1 e) 2 10. De la figura, hallar: Q 2Cos Tan Cos Tan = α + β β α x y a) 1 b) 2 c) 3 d) 4 e) 5 11. Siendo “θ” y ”α” ángulos del II y III cuadrante respectivamente, hallar el signo de: E Sen Cos Tan Cot Sec Csc = θ ⋅ α ⋅ θ θ ⋅ α ⋅ θ a) + b) - c) + y - d) cero e) FD 12. Indicar el signo de: E Sen220 Cos370 Tan265 Sen45 Cos120 Sec240 = ° ° ° ° ° ° a) + b) - c) + y - d) cero e) FD 13. ¿A qué cuadrante pertenece el ángulo “θ"?, si se cumple: Cos θ < Cos( 2 π ) Tan θ > Tan π a) IC b) IIC c) IIIC d) IVC e) FD 14. De la figura, hallar "Tan α"; si: OABC es un cuadrado. O B C A x y a) -2 b) -1/2 c) -1/3 d) -3 e) 1/2 15. Hallar “a”; si: Tan θ = 3 x y (a-1;4a-1) a) –1 b) –2 c) –3 d) –4 e) –5 16. Si: 0 < x < 2π y Sen x = Tan 2π, calcular el valor de: P = Senx2 + Cotx4 + Cscx6 a) 1 b) 2 c) 3 d) 4 e) 0 17. “α" y "β" son complementarios, además se cumple: (Tan α)2 Tan θ+3 = (Cot β)Tan θ+1 Calcular: M = Sen θ + Cos θ ; (θ ∈ IVC) a) 5 5 b)– 5 5 c) 5 10 d)– 5 10 e) 5 15 18. Siendo “θ" un ángulo en posición normal donde: Tan θ = 3 2 − y “Csc θ” es negativo. Calcular: P = 3 + 13 (Sen θ + Cos θ) a) 1 b) 2 c) 3 d) 4 e) 5 19. Si el punto (–a; 3a) pertenece al lado final de un ángulo canónico "θ". Además se cumple que: Cos θ < 0. Calcular: R = Sen θ · Cot θ
EUCLIDES (300 a.C.)
Todo lo que se sabe de Euclides se debe a lo que escribió Proclo (410 - 485), el historiador de la matemática griega.
Nos dice Proclo que Euclides nació en Grecia, a fines del siglo IV a.C., que estudió en la “Academia”, el centro de estudios fundado por Platón en el año 380 a.C, y que enseñó en Alejandría durante el reinado de Ptolomeo I.
Euclides escribió sobre música y sobre óptica, tiene también una obra titulada Sofismas, “para ejercitar la inteligencia”; pero se le conoce más que nada por su obra Elementos, que durante más de veinte siglos se consideró la base de los conocimientos matemáticos en todo el mundo y que todavía hoy se toma como fundamento de los cursos de geometría de la enseñanza media. (Véase Crisis en las matemáticas).
Cuenta Proclo que uno de los discípulos de Euclides se quejaba de la falta de aplicaciones prácticas de los teoremas de la geometría; Euclides ordenó a uno de sus esclavos que le diera una moneda para que sacara algún provecho del estudio de la geometría.
También, cuenta que un día el rey Ptolomeo preguntó si no existía un camino más breve que el de los Elementos para estudiar geometría; la respuesta fue que, en geometría, no existe ningún camino especial para los reyes.