GEOMETRÍA UNI DE EXAMEN DE ADMISIÓN UNIVERSIDAD DE INGENIERÍA SOLUCIONADO PDF
PREGUNTA 1 :
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 2 :
En un triángulo ABC, m∠BAC=2(m∠ACB) = 30°, si se traza la mediana BM, calcule m∠ABM.
A) 75°
B) 80°
C) 90°
D) 100°
E) 105°
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 3 :
El cateto AB del triángulo rectángulo ABC se divide en 8 partes congruentes. Por los puntos de división se trazan 7 segmentos paralelos al cateto AC tal como se muestra en la figura. Si AC= 10 m, halle la suma (en m) de las longitudes de los 7 segmentos.
A) 33
B) 34
C) 35
D) 36
E) 37
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
En un cuadrilátero ABCD, las diagonales miden AC= 17 cm y BD= 15 cm; sea M punto medio de AC y F punto medio de BD; los ángulos interiores de B y D miden 90°. Calcule MF en cm.
A) 2
B) 3
C) 4
D) 5
E) 6
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 :
Al cortarse dos cuerdas de una misma circunferencia perpendicularmente, una de ellas queda dividida en segmentos de 3 y 4 unidades y la otra en segmentos de 6 y 2 unidades. Determine el diámetro de la circunferencia.
A)√87
B)√73
C)√68
D)√65
E)√63
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 6 :
La figura muestra tres semicircunferencias y la longitud de la circunferencia mayor es 10π u. Si AB=√24 u, siendo AB tangente a las semicircunferencias interiores, calcule la longitud (en u) de la circunferencia menor.
A) 2π
B) 3π
C) 4π
D) 5π
E) 6π
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 7 :
Para tres circunferencias tangentes (exteriormente) dos a dos, la suma de sus radios es 10 cm y el producto de los mismos es 40 cm³. Halle el área (en cm²) de la región triangular cuyos vértices son los centros de la circunferencia.
A) 18
B) 18,5
C) 19
D) 19,5
E) 20
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 8 :
El punto A está a 8 m encima de un plano horizontal P, y el punto B se halla a 4 m encima del mismo plano. Si C es un punto del plano P tal que AC+BC es mínimo y el ángulo que forman la recta ↔CB con el plano P es 53°, entonces (en m) AC es
A) 8
B) 8,5
C) 9
D) 9,5
E) 10
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 9 :
Las caras de un triedro equilátero de vértice V miden 60°. En una de sus aristas se considera un punto R de tal manera que VR= 2 cm. Por R pasa un plano perpendicular a VR que interseca a las otras aristas en S y T. Halle el área del triángulo RST (en cm²).
A) 3√2
B) 2√6
C)√26
D) 3√3
E) 4√2
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 10 :
Sea el tetraedro regular de arista a, con a un entero positivo diferente de múltiplo de 3. Se unen los baricentros de las caras del tetraedro regular formando un tetraedro nuevo y así se repite el proceso n veces
A) 8√3
B) 16
C) 8√6
D) 16√2
E) 32
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 11 :
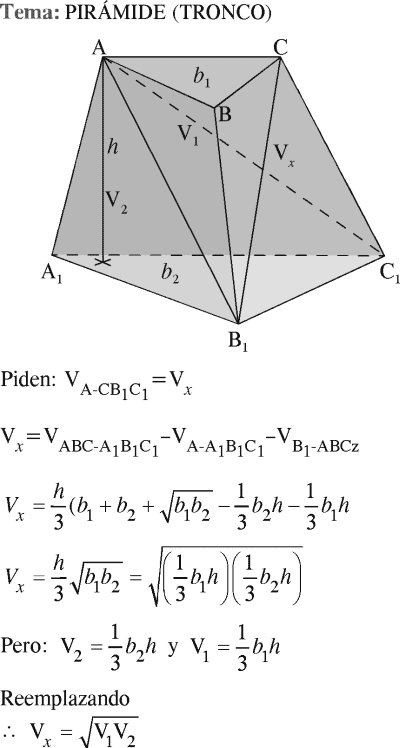
En un tronco de pirámide ABC-A₁B₁C₁, los volúmenes de las pirámides B₁-ABC y A-A₁B₁C₁, miden V₁ y V₂ respectivamente. Determine el volumen de la pirámide A-CB₁C₁.
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 12 :
El volumen de un cono de revolución es 36π cm³. Se inscribe un triángulo equilátero ABC en la base del cono. El triángulo ABC está circunscrito a una circunferencia cuyo círculo es base de un cilindro recto inscrito en el cono. Calcule el volumen del cilindro (en cm³).
A) 27π/10
B) 27π/8
C) 27π/5
D) 27π/2
E) 27π
RESOLUCIÓN :
Rpta. : "D"