TRIGONOMETRÍA UNI DE EXAMEN DE ADMISIÓN UNIVERSIDAD DE INGENIERÍA SOLUCIONADO PDF

PREGUNTA 1 : 

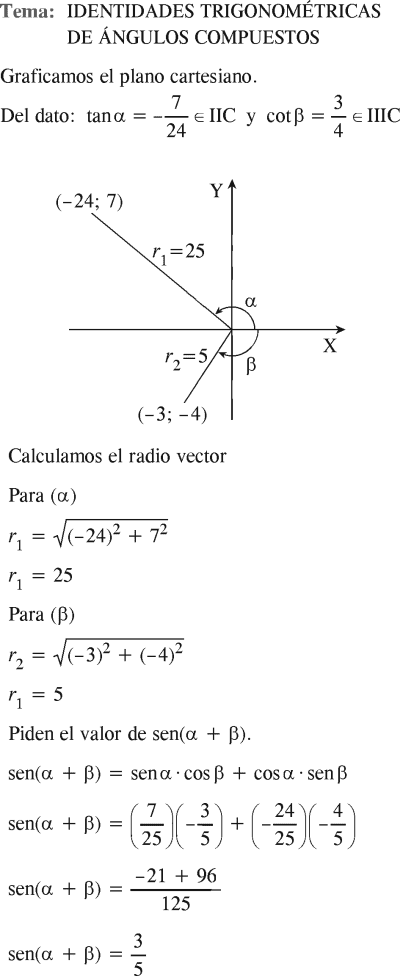
Sea α un ángulo en el II cuadrante con tan(α)=−7/24 y β un ángulo en el III cuadrante con cot(β)=3/4 

Determine el valor de sen(α+β). 

A) − 107/125 

B) − 3/5 

C) 17/125 

D) 3/5 

E) 107/125 

RESOLUCIÓN : 

Rpta. : "D"

PREGUNTA 2 : 

Si la gráfica de y=Aarccos(Bx+C) +D es

determine el valor de E=A+B+C. 

A) 3 

B) 2/3 

C) 4/3 

D) 4 

E) 14/3

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 3 : 

A) 2cos(θ) – sen(θ) 

B) cos(θ) – sen(θ) 

C) 2sen(θ) – cos(θ) 

D) sen(θ) + cos(θ) 

E) sen(θ) – cos(θ) 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 4 : 

Obtenga el conjunto solución del siguiente sistema de ecuaciones: 

y = 1 – cosx 

1 = 4ycosx 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 5 : 

Determine el menor periodo positivo de la función definida por 

A) π/2 

B) π 

C) 3π/2 

D) 2π 

E) 4π 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 6 : 

Un marino que observa el horizonte desde un faro de altura h, lo hace con un ángulo de depresión θ. Calcule el radio R de la Tierra en función de h y θ. 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 7 : 

El menor ángulo de un paralelogramo mide a y sus diagonales miden 2m y 2n. Calcule su área. (m > n) 

A) (m² – n²)tan(α) 

B)(m² – n²)cot(α) 

C) (m² – n²)sec(α) 

D)(m² – n²)csc(α) 

E)(m² – n²)sen(α) 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 8 : 

La ecuación de una cónica en coordenadas polares es

Determine una ecuación cuadrática para sus puntos en coordenadas rectangulares

RESOLUCIÓN :

Rpta. : "B"