HABILIDAD MATEMÁTICA UNMSM PRUEBA DESARROLLADA
PREGUNTA 16 :
Matías tiene varias fichas rectangulares y congruentes como la que se muestra en la figura 1. Distribuyó trece de estas fichas sobre una mesa sin traslaparlas, como se muestra en la figura 2. ¿Cuál es el perímetro de la figura que formó Matías?
A) 184 cm
B) 174 cm
C) 192 cm
D) 198 cm
E) 176 cm
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 17 :
La figura muestra una cuadrícula. Siguiendo las líneas de la cuadrícula y sin repetir punto alguno, ¿cuántas rutas distintas existen para ir desde el punto P hasta el punto Q?
A) 512
B) 128
C) 256
D) 64
E) 360
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 18 :
Los amigos Enrique, José y Santiago tienen S/100, S/110 y S/120, no necesariamente en ese orden. Se sabe lo siguiente:
• José tiene menos soles que Enrique.
• Santiago y Enrique tienen, juntos, S/220.
¿Cuánto suma lo que tienen José, Santiago y la mitad de lo que tiene Enrique?
A) S/280
B) S/270
C) S/265
D) S/275
E) S/285
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 19 :
En un campeonato de fútbol, participaron los equipos Waris, Huancas y Chancas, los cuales jugaron todos contra todos, en una sola ronda. En la tabla, se muestra la cantidad de goles a favor (GF) y goles en contra (GC) de cada equipo al finalizar el campeonato. Si los Waris ganaron a los Huancas por dos goles de diferencia, ¿cuál fue el resultado del partido entre Huancas y Chancas, en ese orden?
A) 5 - 2
B) 2 - 6
C) 6 - 1
D) 2 - 5
E) 4 - 3
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 20 :
Don José tiene una balanza de dos platillos y solo dos pesas: una de 5 kg y otra de 10 kg. Si dispone de más de 100 kg de azúcar, ¿cuántas pesadas, como mínimo, debe realizar don José para obtener 60 kg de azúcar?
A) 3
B) 4
C) 5
D) 2
E) 6
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 21 :
En una pizarra se tiene escrito el siguiente número formado por 2028 cifras:
202820282028...2028
¿Cuál es el máximo número de cifras que se debe borrar para que las cifras que queden sumen 5090?
A) 1004
B) 1000
C) 996
D) 1016
E) 1008
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 22 :
Sin deslizarlo en ningún momento, y a través de su arista, Manuel hace girar un dado normal sobre las casillas cuadradas no transparentes que se muestran en la figura, las cuales coinciden con el tamaño de sus caras. Determine la suma de la cantidad total de puntos visibles para Manuel cuando el dado esté ubicado en la posición final.
A) 17
B) 16
C) 15
D) 18
E) 20
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 23 :
La figura muestra tres balanzas que se encuentran en equilibrio. Los objetos de igual forma y color tienen el mismo peso.
Determine la alternativa con los objetos que se requiere colocar en el platillo M para equilibrar la siguiente balanza:
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 24 :
El reloj de la figura indica la hora en que Francisco sale de su casa, por la mañana, para ir al gimnasio. ¿Qué hora es en ese instante?
A) 6 h 52 min
B) 6 h 51 min
C) 6 h 53 min
D) 6 h 54 min
E) 6 h 55 min
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 25 :
La figura está formada por dos cubos idénticos de mármol con una arista común. Si la arista del cubo mide 10 cm y una hormiga que se encuentra en el vértice P debe pasar por todas las aristas del sólido y terminar su recorrido en el vértice Q, ¿cuál es la mínima longitud del recorrido de la hormiga?
A) 290 cm
B) 300 cm
C) 310 cm
D) 270 cm
E) 280 cm
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 26 :
En la figura, se muestra las vistas frontal, perfil izquierdo y horizontal de un sólido construido de madera de volumen máximo. ¿Cuántas caras tiene dicho sólido?
A) 14
B) 12
C) 15
D) 13
E) 10
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 27 :
Determine la cantidad máxima de cuadriláteros que se pueden contar en la siguiente figura y dé como respuesta la suma de las cifras de dicho resultado.
A) 10
B) 18
C) 12
D) 19
E) 17
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 28 :
En la kermés de un colegio hay un juego para lanzar dardos a un tablero, como el que se muestra en la figura. Para ganar el premio mayor, se tiene que lanzar los dardos y obtener exactamente 104 puntos. Si cada lanzamiento de los dardos cuesta S/15, ¿cuál es la inversión mínima que se debe hacer para ganar el premio mayor?
A) S/150
B) S/135
C) S/180
D) S/165
E) S/195
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 29 :
En la figura, se muestran dos ruedas tangentes cuyos radios miden 12 cm y 8 cm. Si las ruedas se hacen girar en el sentido indicado y A y B son puntos sobre el borde de las ruedas, ¿cuántas vueltas, como mínimo, debe dar la rueda de mayor radio para que los puntos A y B estén en contacto por tercera vez?
A) 23/3
B) 11/3
C) 11/2
D) 8/3
E) 17/3
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 30 :
Mateo tiene una caja con 9000 fichas numeradas desde el 1000 hasta el 9999. ¿Cuántas fichas tiene que extraer al azar, como mínimo y de una en una, para tener la certeza de haber extraído tres fichas cuya suma de los dígitos de los números con las que fueron numeradas sea la misma?
A) 73
B) 72
C) 68
D) 50
E) 72
RESOLUCIÓN :
Rpta. : "B"
SEGUNDA PRUEBA
PREGUNTA 16:
Si el primer día del año 2020 será miércoles y Julio cumple años el 3 de diciembre, ¿qué día de la semana del año 2025 será su cumpleaños?
A) Lunes
B) Miércoles
C) Domingo
D) Martes
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 17:
Tres parejas de esposos, Paul y María, Johnny y Ana, Celso y Eva, se sientan simétricamente alrededor de una mesa de forma circular. Si se sabe que .....
• nunca un hombre se sienta junto a dos mujeres, y que
• las parejas de esposos se sientan juntos excepto Celso y Eva
Señale la afirmación necesariamente correcta.
A) Paul y Johnny se sientan juntos.
B) Celso no se sienta frente a Eva.
C) Ana se sienta junto a Johnny y María.
D) Eva no se sienta junto a Paul.
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 18:
Juan coloca sobre una mesa de madera seis dados convencionales idénticos, tal como se muestra en la figura. ¿Cuántos puntos, como máximo, no son visibles para Juan?
A) 61
B) 68
C) 60
D) 66
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 19:
En el cuadro adjunto se escriben los números 1; 2; 3 y 4 sin repetición, en cada fila, cada columna y cada diagonal. Determine a – b.
A) 3
B) – 3
C) 2
D) – 2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 20:
Escriba en los cuadraditos de la figura los números enteros del 1 al 9, un número en cada cuadradito y, sin repetir, de tal manera que la suma de los números escritos en la fila y columna sea la misma e igual a 27. ¿Cuál es el número que se escribe en el cuadradito sombreado?
A) 9
B) 2
C) 3
D) 5
RESOLUCIÓN :
Rpta. : "A"
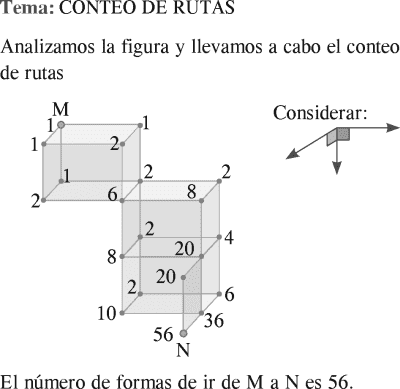
PREGUNTA 21:
La siguiente figura representa una estructura de alambre. Recorriendo solo por las líneas en las direcciones indicadas, ¿de cuántas maneras diferentes se puede ir desde el punto M hasta el punto N?
A) 64
B) 50
C) 48
D) 56
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 22:
Juan compra ocho puertas y recibe nueve llaves distintas, de modo que una de las llaves no abre ninguna puerta y cada una de las ocho restantes abre una puerta distinta. ¿Cuántas veces, como mínimo, Juan tendrá que probar las llaves al azar para saber con certeza a qué puerta corresponde cada llave?
A) 45
B) 44
C) 38
D) 36
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 23:
Un costal está lleno de canicas de 20 colores distintos y de cada uno de los colores hay más de 100 canicas. ¿Cuál es el mínimo número de canicas que se debe extraer al azar para garantizar que en la colección tomada habrá al menos 100 canicas de un mismo color?
A) 1980
B) 1981
C) 2000
D) 2001
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 24:
Un cobrador sale de la oficina y va a realizar sus cobranzas. Primero se desplaza 2,5 km al oeste de la oficina; luego va a un segundo lugar a 4,5 km al norte; de allí continúa 4 km al este y finalmente 6,5 km hacia el sur. ¿A cuántos kilómetros de la oficina se encuentra?
A) 2 km
B) 5 km
C) 3 km
D) 2,5 km
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 25:
En el sistema mostrado, los radios de las poleas M, F, N y G miden 40 cm, 20 cm, 50 cm y 25 cm respectivamente. Si el bloque Q baja 120 cm, ¿qué longitud baja o sube el bloque P?
A) Sube 20 cm.
B) Baja 45 cm.
C) Sube 25 cm.
D) Sube 30 cm.
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 26:
Pedro llegó con 25 minutos de retraso a un examen que duraba 105 minutos y notó que el tiempo que transcurrió desde las 6:00 p.m. hasta que empezó el examen era la cuarta parte del tiempo que transcurriría desde que terminó el examen hasta las 10:00 pm. ¿A qué hora llegó Pedro?
A) 6:52 p.m.
B) 7:52 p.m.
C) 6:42 p.m.
D) 7:42 p.m.
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 27:
¿Qué hora indica el reloj mostrado?
A) 4 h 38 min
B) 4 h 40 min 40 seg
C) 4 h 40 min
D) 4 h 42 min
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 28:
Dada la secuencia de figuras halle x+y.
A) 825
B) 738
C) 804
D) 807
E) 729
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 29:
En la figura se muestra un sistema formado por trece poleas. Si la polea P se mueve en sentido antihorario, ¿cuántas poleas se mueven en sentido horario?
A) 7
B) 5
C) 9
D) 6
RESOLUCIÓN :
Rpta. : "A"
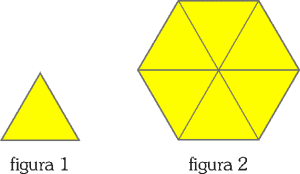
PREGUNTA 30:
Utilizando seis fichas triangulares equiláteras idénticas, como la representada en la figura 1, se ha construido un hexágono regular, como el representado en la figura 2. ¿Cuántas fichas triangulares, como la figura 1, son necesarias para construir otro hexágono semejante a la figura 2 cuyo lado mida el doble que el lado de la figura 2?
A) 24
B) 30
C) 96
D) 48
RESOLUCIÓN :
Rpta. : "A"