GEOMETRÍA EXAMEN DESARROLLADO PRUEBA ADMISIÓN UNIVERSIDAD UNC CLAVES RESPUESTAS SOLUCIONES PREGUNTAS RESUELTAS PDF

PREGUNTA 1 :

El enunciado:

“En toda figura geométrica se puede distinguir : magnitud, forma y posición”

Es:

A) Falso

B) Verdadero

C) Incompleta

D) Absurdo

E) Dudoso

RESOLUCIÓN :

ELEMENTOS FUNDAMENTALES DE LA GEOMETRÍA

Definición

No en todas las figuras geométricas se pueden definir magnitud, forma y posición, esta depende del plano donde se lo considere.

Rpta. : "A"

PREGUNTA 2 :

La afirmación: “Si el área de una esfera es 36𝛑 u², entonces su volumen es 36𝛑 u³ ”. Marcar la alternativa correcta:

A) Ambigua

B) Falsa

C) Imposible

D) Incompleta

E) Verdadera

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 3 :

En la figura, hallar MN, si AB=24 m, NC=20 m y BC=32 m.

A) 10 m

B) 12 m

C) 14 m

D) 15 m

E) 16 m

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 4 :

El perímetro de un triángulo rectángulo es 48 m y su hipotenusa mide 20 m. Hallar la longitud de su inradio.

A) 4 m

B) 5 m

C) 6 m

D) 2 m

E) 3 m

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 5 :

En la figura adjunta, T es punto de tangencia si BC = 4 m y AB= 6 m. Hallar la longitud de R.

A) 15 m

B) 12 m

C) 14 m

D) 16 m

E) 10 m

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 6 :

Calcular el área (en cm²) de la región comprendida entre un círculo y el triángulo inscrito a este, de lados: 7 cm, 24 cm y 25 cm (considere 𝜋 = 3).

A) 468,75

B) 384,75

C) 256,14

D) 318,25

E) 418,32

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 7 :

Calcular el cociente entre el lado y la altura de un triángulo equilátero inscrito en un círculo de radio R.

A) 2√3/3

B) √3/3

C) √3/2

D) √3/4

E) √3/6

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 8 :

¿Cuántos lados tiene un polígono convexo, si al duplicar su número de lados, el número de diagonales aumenta en 84?

A) 9 lados

B) 12 lados

C) 10 lados

D) 8 lados

E) 11 lados

RESOLUCIÓN :

Rpta. : "D"

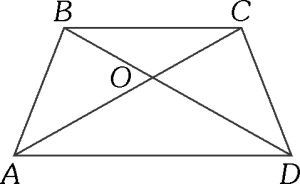
PREGUNTA 9 :

En la figura adjunta, ABCD es un trapecio, donde las diagonales determinan los triángulos AOD y BOC de áreas 25 m² y 16 m², respectivamente. Calcular el área del trapecio.

A) 66 m²

B) 70 m²

C) 81 m²

D) 91 m²

E) 101 m²

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 10 :

Hallar la distancia entre los puntos, cuyas coordenadas son: (0; 3) y (–4; 1).

A) 2√3

B) 2√5

C) 3

D) 5

E) 3√2

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 11 :

En un pentágono convexo ABCDE, AB es perpendicular a BC , BC es perpendicular a CD , m∠D=140° , m∠A=170° . Calcular la m∠E

A) 40º

B) 50º

C) 60º

D) 70º

E) 80º

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 12 :

En un trapezoide ABCD, se tiene: m∠A= 60°; AB = 16√3 cm, CD= 40√2 cm, y m∠D= 45°. Hallar la distancia del punto medio M de BC a AD.

A) 16 cm

B) 18 cm

C) 32 cm

D) 36 cm

E) 64 cm

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 13 :

La proposición:

“Dos ángulos agudos pueden ser suplementarios”

Es:

A) Verdadero

B) Ambigua

C) Probable

D) Falsa

E) Incompleta

RESOLUCIÓN :

ÁNGULOS

Definición

Todo ángulo agudo está comprendido su medida mayor de 0º y menor de 90º, es decir su medida máxima es 89º, por lo tanto, sí consideramos su medida máxima solo sería 178º que no es igual a 180º.

Rpta. : "D"

PREGUNTA 14 :

En la siguiente figura, CD es tangente, CD=2√21cm, AB=diámetro y BC=6cm; hallar la medida del radio de la circunferencia.

A) 1 cm

B) 2 cm

C) 3 cm

D) 4 cm

E) 5 cm

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 15 :

Calcular el área de un segmento circular de 90º de amplitud en un círculo de 10cm de radio (considerar 𝛑 = 3,1416)

A) 28,54 cm²

B) 26,24 cm²

C) 40,04 cm²

D) 24,44 cm²

E) 20,54 cm²

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 16 :

Hallar el radio de la circunferencia de centro O, si AB es perpendicular al plano P.

AF= 12; BO= 17; BA=9

A) 7

B) 17

C) 4

D) 8

E) 6

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 17 :

Uno de los catetos de un triángulo rectángulo mide 40 cm y el radio del circulo inscrito 4 cm. Calcular el área del triángulo en dm².

A) 2,90

B) 1,00

C) 1,80

D) 3,05

E) 3,50

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 18 :

La superficie lateral de un cilindro de revolución es una región cuadrada de área A. Hallar el volumen del cilindro en función de A.

A) (3A√A)/8𝜋

B) (A√A)/8𝜋

C) (A√A)/6𝜋

D) (A√A)/4𝜋

E) (A√A)/2𝜋

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 19 :

Pappus de Alejandria sostiene que “Las abejas ..., en virtud de una cierta intuición geométrica…, saben que el hexágono es mayor que el cuadrado y que el triángulo, y que podrá contener más miel con el mismo gasto de material”; es decir, el hexágono es la figura más eficiente para almacenar la miel. Los hexágonos son regulares, ejemplo, de uno de ellos mide su lado 6cm. Calcular el lado de otro hexágono regular sabiendo que su área es 2/3 del que tiene medida de lado 6 cm.

A) √6 cm

B) 2√6 cm

C) 3√6 cm

D) 6√2 cm

E) 2√3 cm

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 20 :

Se tiene un trapecio ABCD cuyas diagonales se cortan perpendicularmente; si la base mayor AD es igual a la diagonal AC e igual a 4 cm. Calcular la longitud de la base menor BC , BD= 3 cm.

A) 1 cm

B) 2 cm

C) 3 cm

D) 4 cm

E) 5 cm

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 21 :

Calcular la base del rectángulo mostrado, si AB=3m, BC=9m y CD=16m.

A) 20m

B) 22m

C) 24m

D) 26m

E) 28m

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 22 :

Calcular la longitud del radio de la circunferencia mostrada, si O = centro, AD=OD , ED =4u , CD=8u

A) 2 u

B) 4 u

C) 6 u

D) 8 u

E) 10 u

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 23 :

Los lados de un cuadrilátero inscrito en una circunferencia miden 7u, 15u, 20u y 24u respectivamente; hallar la longitud de cada una de las diagonales de dicho cuadrilátero.

A) 15u y 23u

B) 18u y 20u

C) 15u y 10√7 u

D) 8√3 u y 24u

E) 20u y 25u

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 24 :

En un romboide ABCD; AB=12m, BC=16m . Se traza la bisectriz interior del ángulo A, la cual intersecta a BC en E y a la prolongación de DC en F; si se traza desde M punto medio de EF un rayo paralelo a CD, interceptado a AD en N. Hallar la longitud del segmento MN .

A) 12 cm

B) 20 cm

C) 18 cm

D) 14 cm

E) 16 cm

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 25 :

El área de la base de una pirámide cuadrangular es de 16 m² y su apotema mide 2√3m. Hallar el área de la superficie total de la semiesfera inscrita en dicha pirámide, si se sabe que el circulo máximo está contenido en la base de la pirámide.

A) 10𝛑m²

B) 12𝛑m²

C) 14𝛑m²

D) 9𝛑m²

E) 8𝛑m²

RESOLUCIÓN :