RAZONAMIENTO LOGICO UNT EXAMEN ADMISION UNIVERSIDAD DE TRUJILLO DESARROLLADO PDF
PREGUNTA 1 :
En la proposición:
En forma alguna, en cuanto el juez dicte sentencia de divorcio absoluto, el matrimonio se disuelve.
Equivale a:
A) El matrimonio se disuelve cuando el juez dicte sentencia de divorcio.
B) El juez dicta sentencia de divorcio absoluto pero el matrimonio no se disuelve.
C) Siempre que un matrimonio se disuelve, es porque se dictó sentencia.
D) Se dicta sentencia de divorcio cuando solo y cuando el matrimonio se disuelve.
E) No se dicta sentencia de divorcio porque el matrimonio se disuelve.
RESOLUCIÓN :
EQUIVALENCIAS LÓGICAS
Formalizamos: ∼(D → M) ≡ D ∧ ∼ M
Por lo tanto, la proposición equivale a
“El juez dicta sentencia de divorcio absoluto pero el matrimonio no se disuelve”
Rpta. : "B"
PREGUNTA 2 :
Son proposiciones coligativas:
1. Juan y Mario son miembros del Comité de Defensa Civil.
2. Juan no obstante Mario no son miembros del Comité de Defensa Civil.
3. Juan conjuntamente con Mario ambos forman el Comité de Defensa Civil.
4. Juan y Mario juntos van al colegio.
5. 14 además 15 son números pares.
Son ciertas:
A) 1, 3 y 5
B) 2, 4 y 5
C) 1, 2 y 5
D) 3, 4 y 5
E) 2, 3 y 4
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 3 :
La relación de conceptos:
Corresponde a una inclusión total:
1. Hay zarigüeyas que son marsupiales.
2. Toda zarigüeya es marsupial.
3. Cada una de las zarigüeyas no deja de ser marsupial.
4. Cualquier marsupial es zarigüeya.
5. Hay zarigüeyas que no son marsupiales.
Son ciertas:
A) 1, 2 y 3
B) 1, 4 y 5
C) 2, 3 y 4
D) solo 4 y 5
E) solo 2 y 3
RESOLUCIÓN :
CONCEPTO Y TÉRMINO
Se deduce: Toda zarigüeya es marsupial.
Analizando:
1. Falso
2. Verdadero
3. Verdadero
4. Falso
5. Falso
Rpta. : "E"
PREGUNTA 4 :
De las premisas
P1: ∀x(Ax → Bx)
P2: ∃x(Cx ∧ Bx)
Se infiere:
A) Todo no C es no A.
B) Ningún C es no A.
C) Ni siquiera un C es A.
D) Algún C es A.
E) Todo C es A.
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 :
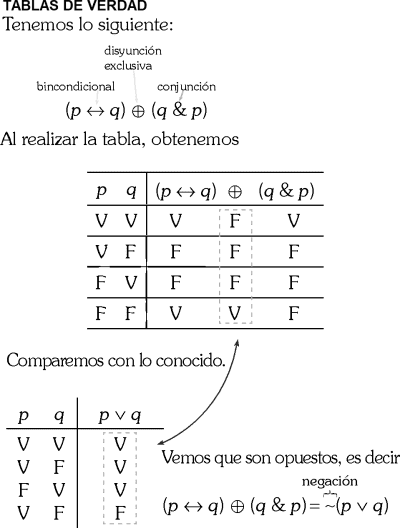
De la siguiente tabla de verdad:
Afirmamos lo siguiente:
1. La fórmula inferencial se encuentra ubicada en el margen superior.
2. Presenta en el margen inferior la variable p cuatro valores de verdadero.
3. La matriz final del esquema demuestra que es un principio lógico.
4. La fórmula inferencial se encuentra ubicada en el cuerpo superior.
5. La fórmula inferencial representa la regla del afirmando afirma.
Son ciertas:
A) 1, 2 y 3
B) 1, 3 y 5
C) 2, 3 y 4
D) 2, 4 y 5
E) 3, 4 y 5
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 6 :
De los siguientes conceptos:
1. Android - Sistema Operativo
2. Laptop - Computador Personal
3. Profesión - Informática
Se puede afirmar que una conclusión falsa es
A) Android es subordinado de Sistema Operativo.
B) Computador Personal es subordinante de Laptop.
C) Informática es subordinado de Profesión.
D) Android no es comparable con Laptop.
E) Informática no es comparable con Computador Personal.
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 7 :
RESOLUCIÓN :
Rpta. : "C"
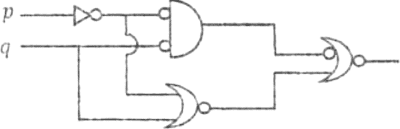
PREGUNTA 8 :
El circuito lógico adjunto:
Se formaliza:
A) ∼[∼(∼ p ∧ ∼ q) ∨ ∼(∼ p ∧ q)]
B) ∼[∼(p ∧ ∼ q) ∨ ∼(∼ p ∨ q)]
C) ∼[∼(p ∧ ∼ q) ∨ ∼(∼ p ∧ q)]
D) ∼[∼(∼ p ↓ q) ∨ ∼(∼ p ∨ q)]
E) ∼[∼(∼ p ↓ ∼ q) ∨ ∼(∼ p ∨ q)]
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 9 :
La proposición: “El que los nazcas hayan construido una red de canales es suficiente para distribuir el agua de los ríos y de los acueductos subterráneos. En tal sentido los canales estaban a más de diez metros de profundidad y medirán aproximadamente un metro de ancho”.
Se formaliza:
A) [p ← (q ∧ r)] → (s ∧ t)
B) [p → (q ∧ r)] → (s ∧ t)
C) [p ← (q ∨ r)] → (s ∧ t)
D) [p → (∼ q ∧ r)] → (s ∧ t)
E) [p →(q ∧ r)] → (s ∧ t)
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 :
De la expresión Nadie es feliz, inferimos:
1. Es falso que todos sean felices.
2. Ni Andrea ni Elena son felices.
3. Es absurdo que algunos sean felices.
4. Nicolasa no es feliz a menos que Maritza no sea feliz.
5. Es mentira que hay felices.
Son ciertas:
A) 2, 3 y 4
B) 2, 3 y 5
C) 3, 4 y 5
D) 1, 2 y 3
E) 1, 3 y 5
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 11 :
De la expresión:
"Casi no hay lógicos", podemos obtener equivalentemente en un universo finito:
1) Max o Santiago son lógicos.
2) Luis es lógico o también Gustavo es lógico.
3) Si Jacinto no es lógico, Ervando sí lo es.
4) Es una farsa que, ni Walter ni Carlos sean lógicos.
5) Elvis es lógico en el caso de que Víctor no lo sea.
SON CIERTAS:
A) solo 1, 3 y 5
B) solo 3, 4 y 5
C) solo 2 y 4
D) solo 2 y 5
E) todas
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 12 :
Caracterizan al lenguaje formal:
1. Tiene significado conceptual.
2. Su verdad es convencional.
3. Sus símbolos o reglas carecen de contenido conceptual.
4. Su significado es el objeto.
5. Es condición suficiente para el conocimiento científico.
Son ciertas:
A) 1, 2 y 3
B) 3, 4 y 5
C) 2, 3 y 4
D) 1, 2 y 5
E) 2, 3 y 5
RESOLUCIÓN :
PENSAMIENTO Y LENGUAJE
Características del lenguaje formal:
1. Tiene significado conceptual (F)
2. Su verdad es convencional (V)
3. Sus símbolos o reglas carecen de contenido conceptual (V)
4. Su significado es el objeto (V)
5. Es suficiente para el conocimiento (F)
Rpta. : "C"
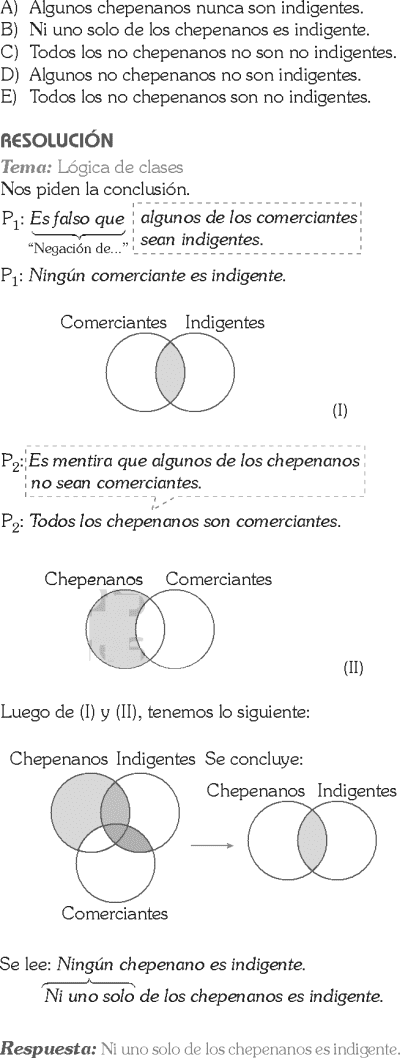
PREGUNTA 13 :
Dadas las premisas:
“Algunos psicólogos son docentes, además, muchos de los no psicólogos son docentes, pero, varios de los no docentes son psicólogos”, se infiere:
A) Todos son psicólogos o docentes, salvo que, sean docentes y psicólogos.
B) Todos son psicólogos o docentes, además, sean docentes y psicólogos.
C) Todos son psicólogos o docentes, salvo que, sean docentes pero no psicólogos.
D) Todos son psicólogos o docentes, salvo que, ni son docentes ni psicólogos.
E) Todos son psicólogos o docentes, además, sean psicólogos pero no docentes.
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 14 :
Pedro es un alumno aplicado que asistió a un seminario de Razonamiento Lógico; de allí salió muy preocupado por lo que dijo el profesor al final de la clase: “Quienquiera que piense con Lógica es coherente”; de allí que tenía que hacer varias inferencias correctas para entender dicho enunciado, estas fueron:
1. Es falso que hay no coherentes y no piensan con lógica.
2. Es objetable que casi la totalidad que es coherente piensa con lógica.
3. Ninguno que es incoherente no piensa con lógica,
4. Ni algún incoherente piensa con lógica.
5. Si no es coherente, evidentemente no piensa con lógica.
Son ciertas:
A) 1, 2 y 3
B) 3, 4 y 5
C) 1, 2 y 5
D) Solo 4 y 5
E) Solo 1 y 4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 15 :
Del diagrama
Donde:
E=Empresarios
F=Futbolistas
Se infiere:
1. Es absurdo que no haya futbolistas que no sean empresarios.
2. En modo alguno ocurre que ni siquiera un no empresario sea futbolista.
3. Bastantes no futbolistas de seguro no dejan de ser empresarios.
4. Muchos que no son empresarios no son sin duda no futbolistas.
5. No casi hay no futbolistas que de algún modo sean empresarios.
Son ciertas:
A) 1, 2 y 5
B) 1, 2 y 4
C) 1, 3 y 4
D) 2, 3 y 5
E) 3, 4 y 5
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 16 :
De los siguientes esquemas:
1. p → ~ (p ∨ q) =~ p
2. {(p ∨ q) ∧ [∼ (∼ p ∧ ∼ q) ∨ r]} ↔ (p ∨ q)
3. (p ∨ q) ⊕ ~ (p ∧ ~ q)
4. ~ [p → (q ∧ p)] ↓ ~ p
5. ~ [~ p ∧ p) ∨ 0]
son tautológicos:
A) 1, 2 y 5
B) 2, 3 y 4
C) 1, 3 y 5
D) 1, 2 y 4
E) 3, 4 y 5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 17 :
Si
“Algunos políticos no son chauvinistas”,
“Ciertos chauvinistas no son políticos”,
“Hay políticos que son chauvinistas”;
se induce que:
A) Todo político es chauvinista.
B) Cualquier chauvinista es político.
C) Muchos políticos no son chauvinistas.
D) Quienquiera es político o chauvinista o político y chauvinista.
E) Ningún hombre es político o chauvinista, o, ni político ni chauvinista.
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 18 :
De las siguientes premisas:
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 19 :
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 20 :
De los siguientes enunciados:
1. Nacionalismo es lo mismo que chauvinismo.
2. Neoliberal es lo mismo que inhumano.
3. El que juegue es lo mismo que me divierta.
4. Si no hay recesión entonces los sueldos aumentarán.
5. 256 > 128 es equivalente a 1024 > 512.
Son proposiciones coimplicativas:
A) 1, 2 y 4
B) 1, 2 y 5
C) 2, 3 y 4
D) 3 y 5
E) solo 3
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 21 :
De la proposición “casi no hay policías”, en un universo finito, se obtiene:
1. Álex o Santiago son policías.
2. Luis es policía o también Francisco es policía.
3. Si Elidio no es policía, Orlando sí lo es.
4. Es una farsa que, ni Walter ni Carlos sean policías.
5. Elvis es policía únicamente si Víctor no lo es.
Son ciertas:
A) solo 1, 3 y 5
B) solo 2 y 5
C) solo 2 y 4
D) solo 3, 4 y 5
E) 1, 2, 3, 4 y 5
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 22 :
La premisa:
“Existen médicos que son ginecólogos” equivale a:
1. Es absurdo que casi ningún médico es ginecólogo.
2. Es falso que todos los ginecólogos son no médicos
3. En absoluto sucede que ningún ginecólogo es médico.
4. Existen ginecólogos que son médicos.
5. Todos los médicos son no ginecólogos.
Son ciertas:
A) 1, 2 y 3
B) 2, 3 y 4
C) 3, 4 y 5
D) 1 y 4
E) 2 y 5
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 23 :
Son características del lenguaje formal :
1. tiene múltiples significados ·
2. solamente es escrito
3. fue creado con fines prácticos
4. posee una gramática imperfecta
5. sus símbolos tienen sonidos propios
SON CIERTAS:
A) 1 ,2 y 5
B) 1 ,3 y 5
C) 3, 4 y 5
D) 2 y 3
E) solo 3 y 5
RESOLUCIÓN :
PENSAMIENTO Y LENGUAJE
Solamente es escrito y fue creado con un fin práctico.
Por lo tanto, son ciertas 2 y 3.
Rpta. : "D"
PREGUNTA 24 :
Dado el esquema verdadero:
–{[(p ∨ –q) ∧ r]/[(–r ← p) ↓ –q]};
los valores de verdad de las fórmulas:
I (–s ∨ q) → (–p ∧ r)
II. (–p ← q) ⊕ (–r ∨ p)
III. (s ∧ –t)/[(p ∧ –q) ↓ r]
Son respectivamente:
A) 111
B) 000
C) 110
D) 011
E) 010
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 25 :
El circuito adjunto:
equivale a
A) p
B) q
C) r
D) s
E) – s
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 26 :
El circuito lógico;
Se obtiene un circuito lógico equivalente a la fórmula:
A) p ∨ – p
B) q ∨ q
C) ¬ p ⊕ q
D) p ↓ q
E) p \ q
RESOLUCIÓN :
Rpta. : "C"
