RAZONAMIENTO MATEMÁTICO EXAMEN DESARROLLADO PRUEBA ADMISIÓN UNIVERSIDAD UNC CLAVES RESPUESTAS SOLUCIONES PREGUNTAS RESUELTAS PDF

PREGUNTA 1 :

Si ✎a= a(a – 1)

Calcular ✎(✎7)

A) 243

B) 200

C) 2100

D) 1722

E) 1850

RESOLUCIÓN :

(✎7)=7×6=42

⇒ ✎(42)=42×41=1722

Rpta. : "D"

PREGUNTA 2 :

Hallar el valor de x en:

A) 1

B) 3

C) 5

D) 4

E) 8

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 3 :

Sea : a █ b ▀f(x) = f(a + b) – f(a – b)

Para f(x) = 4x + 3

Calcular el valor de E=3 █ 1 ▀f(x)

A) 7

B) 8

C) 10

D) 9

E) 11

RESOLUCIÓN :

E=3 █ 1 ▀f(x)= f(3 + 1) – f(3 – 1)

= f(4) – f(2)=4(4) + 3 – [4(2) + 3 ]

= 19 – 11 = 8

Rpta. : "B"

PREGUNTA 4 :

Determinar el número que sigue en la serie:

3 ; 5 ; 9 ; 17 ; 33 ; …

A) 66

B) 34

C) 60

D) 65

E) 63

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 5 :

La proposición más simple equivalente a:

[(~ q → ~ p) → (~ p → ~ q)] ∧ ~ ( p ∧ q), es:

A) ~ p

B) ~ q

C) p ∧ q

D) p ∨ ~ q

E) p ∧ ~ q

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 6 :

Indicar la letra que sigue en la serie:

W ; U ; R ; Ñ ; …

A) L

B) R

C) I

D) J

E) O

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 7 :

Según el gráfico que se muestra, ¿qué se puede afirmar sobre los gastos de la persona si esta tiene un ingreso de S/1200?

I. La persona gasta S/180 en otros.

II. Gasta igual en viviendo que en ropa.

III. En alimentación gasta S/360.

A) solo I

B) solo II

C) solo III

D) I y II

E) I y III

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 8 :

El siguiente gráfico muestra las notas de un alumno del 5.° grado de secundaria, obtenidas cada mes:

¿En qué porcentaje bajó su nota en setiembre, con respecto al mes de mayo?

A) 21,43%

B) 24,23%

C) 25,33%

D) 26,67%

E) 27,56%

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 9 :

Se tiene una hoja de papel de forma cuadrada, cuyo lado mide 36 cm de longitud, se dobla por la mitad y se vuelve a doblar por la mitad para obtener una tarjeta cuadrada. ¿Cuál es el perímetro de dicha tarjeta?

A) 36 cm

B) 40 cm

C) 64 cm

D) 72 cm

E) 32 cm

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 10 :

La negación de la siguiente proposición:

“Todo número real tiene un único inverso aditivo”

es...

A) Existe un número real con único inverso aditivo.

B) Todo número real no tiene inverso aditivo.

C) Todo número real admite dos inversos aditivos.

D) Existe un número real que tiene por lo menos dos inversos aditivos.

E) Existe un número real cuyo inverso aditivo no existe.

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 11 :

Indicar qué letra continúa en la siguiente serie:

B ; Q ; P ; C ; S ; R ; D ; U ; ...

A) O

B) P

C) T

D) R

E) M

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 12 :

Hallar el valor de U + N + C

Si:

A) 11

B) 12

C) 13

D) 14

E) 15

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 13 :

Qué combinación de letras continúa :

AB ; BD ; DG ; GK ; …

A) KO

B) PQ

C) RS

D) ST

E) PO

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 14 :

¿Cuántas banderas tricolores se pueden diseñar si se disponen de 6 colores de telas?

A) 120

B) 150

C) 100

D) 40

E) 15

RESOLUCIÓN :

Por el principio de multiplicación para encontrar el total de banderas tricolores.

Por lo tanto, se pueden obtener 120 banderas tricolores.

Rpta. : "A"

PREGUNTA 15 :

Hallar el valor de verdad de las proposiciones:

I. (0⁰ = 1) ↔ (– 5 < – 10)

II. (1+1≠1) → ( √2 = 2)

III. log100=2 ∧ sen𝛑/6=1/2

A) FVF

B) FFV

C) VFV

D) VVF

E) VFF

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 16 :

En el siguiente cuadro, determinar el número que falta:

A) 600

B) 450

C) 250

D) 800

E) 1050

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 17 :

Se inscribe un círculo en un triángulo equilátero y se inscribe un cuadrado en el círculo. La razón del área del triángulo al área del cuadrado es:

A) 3√3/2

B) √3/4

C) 3/2

D) 1/2

E) 2√3/2

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 18 :

En una reunión del centro PRE hay 24 personas, de las cuales 3 son personal administrativo y el resto son personal docente. ¿De cuántas formas diferentes se puede formar una comisión de 3 miembros de manera que, en cada comisión haya por lo menos un personal administrativo?

A) 696

B) 669

C) 684

D) 694

E) 649

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 19 :

Dadas las funciones reales:

Si D(f) ∩ D(g) ≠ ∅, existe la adición de dichas funciones.

Hallar D(f) ∩ D(g).

A) 〈– ∞; –2] ∪ [2; +∞〉

B) [–1; 1]

C) [–2; –1] ∪ [1; 2]

D) 〈– ∞; – 2] ∪ 〈1; +∞〉

E) [–2; 2]

RESOLUCIÓN :

Rpta. : "C"

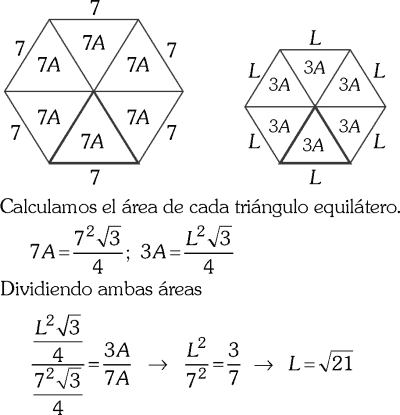
PREGUNTA 20 :

El lado de un hexágono regular mide 7 m. Determinar cuánto mide el lado de otro hexágono cuya área es 3/7 del área del primer hexágono.

A) √28 m

B) √20 m

C) √22 m

D) √21 m

E) √29 m

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 21 :

En la figura, calcular la medida del ángulo x, si se sabe que BC=AB, BM=BN

A) 18°

B) 20°

C) 15°

D) 10°

E) 12°

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 22 :

¿Cuántas combinaciones de tres letras distintas que comienzan con la letra P, pueden obtenerse con las letras: P, Q, R, S?

A) 5

B) 7

C) 8

D) 6

E) 9

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 23 :

Se quiere elegir una junta directiva de APAFA en una institución educativa conformada por 6 integrantes: un presidente, un vicepresidente, un secretario, un tesorero y dos vocales, ¿de cuantas maneras se puede elegir la junta si se presentan 10 candidatos?

A) 210

B) 60

C) 720

D) 840

E) 180

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 24 :

¿De cuántas maneras se pueden colocar 7 niños en una fila, de manera que 3 niños en particular queden juntos?

A) 120

B) 5040

C) 900

D) 720

E) 840

RESOLUCIÓN :

Rpta. : "D"

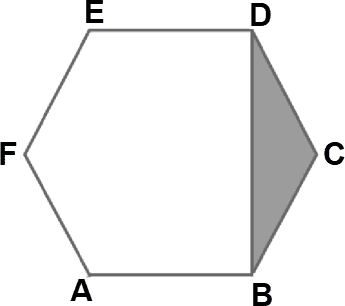
PREGUNTA 25 :

La figura ABCDEF es un hexágono regular y el área sombreada mide 16√3 m² , el perímetro del hexágono es:

A) 6√3m

B) 18m

C) 4√5m

D) 48m

E) 16√5 m

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 26 :

Si : a – b = 5

Expresa (a – 4)(a + 3) en función de b

A) (b – 1)(b + 3)

B) (b + 1)(b + 8)

C) (b – 1)(b – 3)

D) (b – 1)(b + 8)

E) (b + 1)(b – 8)

RESOLUCIÓN :

a – b = 5 ⇒ a = 5 + b

Reemplazando en lo pedido :

(a – 4)(a + 3) = ( 5 + b – 4)( 5 + b + 3) = (b + 1)(b + 8)

Rpta. : "B"

PREGUNTA 27 :

Hallar el valor numérico de “x” en la siguiente ecuación:

(a + 3)x + (b + 4)x + 5 = 5

Información brindada:

I. a = − 4 ∧ b = − 3

II. a + b = 8

Para resolver el problema:

A) La información I es suficiente.

B) La información II es suficiente.

C) Es necesario utilizar ambas informaciones.

D) Cada una de las informaciones por separado, es suficiente.

E) Las informaciones dadas son insuficientes.

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 28 :

Las tres cuartas partes de n² es 12. Entonces el perímetro de un triángulo equilátero de lado n unidades es:

A) 4u

B) 12u

C) 16u

D) 24u

E) 36u

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 29 :

Se quiere cercar con seis vueltas de alambre un jardín de forma rectangular sabiendo que sus lados tienen la siguiente relación, el largo excede en 8 m al acho; además su área es de 3120 m², y el precio del metro de alambre es de S/.12. Hallar el costo total para cercar el jardín

A) S/. 224

B) S/. 2688

C) S/. 16128

D) S/. 3120

E) S/. 8064

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 30 :

¿Cuántos números de 4 dígitos pueden formarse con los dígitos: 0, 1, 2, 3, 4, 5 y 6; considerando que no se permite la repetición de dígitos?

A) 120

B) 360

C) 540

D) 720

E) 1 440

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 31 :

¿Cuántos números de 4 cifras menores que 2367 se pueden formar con los dígitos 1 , 2 , 3 y 4, si cada digito se usa una sola vez?

A) 20

B) 12

C) 16

D) 10

E) 14

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 32 :

Tres números son entre sí como 2 ; 5 y 7 respectivamente, La suma de estos tres números es 420. ¿Cuál de ellos es el número menor?

A) 30

B) 150

C) 60

D) 120

E) 70

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 33 :

Si en una proporción geométrica continua, la media geométrica es 24 y la razón es 2/3 indicar la diferencia de los extremos.

A) 18

B) 20

C) 24

D) 16

E) 14

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 34 :

Las edades de los estudiantes Esteban y Javier son dos números pares consecutivos, cuyo producto es menor o igual a 728. Hallar la suma de las cifras de la edad del estudiante de mayor edad.

A) 2

B) 4

C) 6

D) 8

E) 10

RESOLUCIÓN :

PLANTEO DE INECUACIONES

Esteban: 2x – 2

Javier: 2x

(2x – 2)(2x) ≤ 728

2(x – 1)(2x) ≤ 728

(x – 1)x ≤ 182

(x – 1)x ≤ 13×14

Tanteando adecuadamente :

x = 14

Piden

El mayor: 2x=28

⇒ 2 + 8 = 10

Rpta. : "E"

PREGUNTA 35 :

Calcular la media proporcional de dos cantidades, si la diferencia de los extremos es 65 y la suma de los cuadrados de los cuatro términos de la proporción geométrica continua es 5625

A) 3√14

B) 5√14

C) 4√14

D) 5√15

E) 4√15

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 36 :

Si:

Hallar el valor de: a×b×c

A) 3080

B) 2050

C) 2850

D) 3280

E) 1350

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 37 :

Hallar la mediana para el siguiente conjunto de datos.

140 ; 6 ; 28 ; 101 ; 12 ; 48 ; 1860 ; 32 ; 964 ; 76

A) 48,0

B) 76,0

C) 62,0

D) 163,5

E) 362,3

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 38 :

Se lanza un dado 100 veces. La siguiente tabla muestra los seis números y la frecuencia con que cada uno ha aparecido.

Encontrar la frecuencia relativa del suceso en que aparece un número impar.

A) 31%

B) 49%

C) 50%

D) 53%

E) 61%

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 39 :

Para el enunciado :

“Ni eres buen hijo ni buen estudiante”

Su forma negada equivale a:

A) No eres buen hijo y buen estudiante.

B) Eres buen hijo y buen estudiante.

C) No eres buen hijo o no eres buen estudiante.

D) Eres buen hijo o no eres buen estudiante.

E) Eres buen hijo o eres buen estudiante.

RESOLUCIÓN :

p : buen hijo

q : buen estudiante

Piden : ~ (~ p ∧ ~ q) ≡ p ∨ q

Rpta. : "E"

PREGUNTA 40 :

Sean:

p : “Gané una beca”

q : “Viajo al extranjero”.

Simplificando y luego traduciendo la proposición:

[( p∨ ~ q) ∨ (~ p ∧ q)∨ q] ∧ q

Equivale a:

A) Gano una beca.

B) Viajo al extranjero

C) No gano una beca

D) No viajo al extranjero.

E) Gano una beca y viajo al extranjero.

RESOLUCIÓN :

Por ley asociativa :

{ [( p∨ ~ q) ∨ (~ p ∧ q)] ∨ q } ∧ q

Por ley de absorción :

≡ q ≡ Viajo al extranjero

Rpta. : "B"

PREGUNTA 41 :

Si se sabe que: (p Λ q) y (q → t) son falsas,

¿Cuáles de las siguientes proposiciones son verdaderas?

I.( ~ p V t) V s

II. ~ [p Λ (~ p V ~ q)]

III. [ ~ p V (q Λ ~ t] ↔ [(p → q) Λ ~ (q Λ t) ]

A) I

B) II

C) Todas

D) I y II

E) II y III

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 42 :

Determinar el valor de “M + N” en la serie:

6 ; 3 ; 20 ; 8 ; 42 ; 15 ; M ; N

A) 84

B) 86

C) 96

D) 98

E) 106

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 43 :

Si se sabe que:

– Todo periodista es crítico.

– Algunos periodistas son profesionales objetivos.

Se concluye que:

A) Todo periodista no es crítico"'

B) Ningún crítico es profesional objetivo.

C) Algún profesional objetivo no es periodista.

D) Algunos profesionales objetivos son críticos.

E) Algunos periodistas son profesionales objetivos.

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 44 :

¿Qué letras completan la serie?

HBC ; LFG ; PJK ; ... ; XRS

A) SLM

B) WNM

C) VON

D) UMO

E) TNO

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 45 :

Determinar la letra que continúa en la secuencia:

P ; N ; K ; I ; F ; D ; …

A) C

B) B

C) A

D) D

E) E

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 46 :

La siguiente tabla muestra las edades de 220 estudiantes de una institución educativa.

I. La moda es 17 años.

II. La mediana es mayor que la media (promedio).

III. La mitad de los estudiantes de la institución educativa tiene 17 o 18 años.

¿Cuál o cuáles son verdaderas?

A) I

B) II

C) I y II

D) II y III

E) Todas

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 47 :

La negación de ∃x / P(x) ∨ ~ Q(x) es:

A) ∃x/~ P(x) ∨ Q(x)

B) ∀x : ~ P(x) ∨ Q(x)

C) ∃x / P(x) ∧~ Q(x)

D) ∀x :~ P(x) ∧ Q(x)

E) ∀x : P(x) ∧~ Q(x)

RESOLUCIÓN :

~｛∃x / P(x) ∨ ~ Q(x) ｝≡ ∀x :~ P(x) ∧ Q(x)

Rpta. : "D"

PREGUNTA 48 :

La proposición:

“La mayoría de narcotraficantes son deshonestos”

Equivalente a:

A) Cualquier narcotraficante no es deshonesto.

B) Todos los narcotraficantes son deshonestos.

C) No es verdad que, ningún narcotraficante es deshonesto.

D) Ciertos no narcotraficantes innegablemente no son deshonestos.

E) Para cada narcotraficante se verifica que es deshonesto.

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 49 :

La proposición:

“No es inadmisible que, para cada médico teórico se compruebe que es intelectual”, equivale a:

A) ∀x : [ R(x) → S(x) ]

B) ~[ ∀x : R(x) → S(x) ]

C) ~[ ∃x / R(x)∧ ~S(x) ]

D) ∃x /[ R(x) ∧ S(x) ]

E) A y C

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 50 :

Dado el argumento:

Si llueve, me resfrío

Si me resfrío, no asistiré a clases

Asisto a clases

-----------

Se concluye que:

A) Llueve

B) No llueve

C) Me resfrío

D) No me resfrío

E) Llueve y no me resfrío

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 51 :

Sean:

P(x) = ”x es impar”

Q(x) = ”x divide a 3”.

Siendo Z el conjunto de los números enteros, la negación de la proposición :

∀x∈Z:[ P(x) ∧ Q(x) ]

Se traduce:

A) Todos los números enteros son impares o no dividen a 3.

B) Algunos números enteros son impares o no dividen a 3.

C) Hay enteros que no son impares, pero dividen a 3.

D) Existen enteros que no son impares o no dividen a 3.

E) Todos los enteros, si son impares dividen a 3.

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 52 :

Determinar cuáles de las siguientes proposiciones son equivalentes a:

“No es verdad que ningún congresista es honesto”.

1) Existe honestos que son congresistas

2) Algunos no honestos son congresistas

3) Es falso que, cualquier no es congresista o no es honesto

4) Cualquiera es honestos o no es congresista

5) La mayoría de congresista son honestos

A) 1, 2 y 5

B) 1, 3 y 5

C) 1, 2 y 4

D) 2, 3 y 5

E) 3, 4 y 5

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 53 :

Hallar el perímetro de un triángulo rectángulo, si la altura relativa a la hipotenusa mide 24 cm y la diferencia de las proyecciones ortogonales de sus catetos sobre la hipotenusa es 14 cm.

A) 576 cm

B) 400 cm

C) 225 cm

D) 2 500 cm

E) 120 cm

RESOLUCIÓN :