RAZONAMIENTO MATEMATICO UNT EXAMEN ADMISION UNIVERSIDAD DE TRUJILLO DESARROLLADO PDF
PREGUNTA 1 :
El sueldo de un trabajador es proporcional al cuadrado de la edad que tiene; si actualmente tiene 25 años, el número de años que deben transcurrir para que cuadruplique su sueldo es:
A) 30
B) 25
C) 20
D) 15
E) 10
RESOLUCIÓN :
EDADES - MAGNITUDES PRPORCIONALES :
Por el dato, el sueldo del trabajador es proporcional al cuadrado de su edad:
Sueldo=(Edad)²K
Además, se sabe que:
Edad actual =25 años → Sueldo actual = (25)²K=625K
Deseamos que el sueldo se cuadruplique:
Nuevo sueldo=(Nueva edad)²K=4(625K)
Nuevo sueldo=(Nueva edad)²K=2500K
(Nueva edad)²K=50²K
Entonces la nueva edad sería 50 años.
Por lo tanto, debe transcurrir: (50 – 25) =25 años
Rpta. : "B"
PREGUNTA 2 :
A) – 1
B) – 2
C) – 3
D) – 4
E) – 5
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 3 :
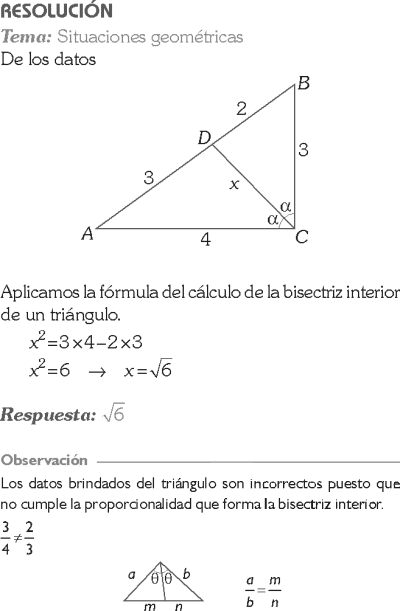
Dado el cuadrilátero convexo ABCD, se sabe que AB= 4 unidades, BC=5 unidades, CD=6 unidades, AD=3 unidades y el ángulo interior del vértice A forma un ángulo recto. El área de la región ABCD, en unidades cuadradas, es:
A) 16
B) 18
C) 20
D) 24
E) 30
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
A) 8
B) 10
C) 12
D) 13
E) 21
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 5 :
A) 3/10
B) 10/3
C) 5/2
D) 2/5
E) 3/2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6 :
Una casa se vende recargándose el m% del precio de costo, pero un ingeniero al comprarla le rebajaron el n%. Si el vendedor no ganó ni perdió, entonces el valor de “n” equivale a:
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 7 :
Fabiano va a doblar en forma de un rectángulo un alambre de 14 m de largo con la condición de que la diagonal de dicho rectángulo mida menos de 5 m. La medida, en metros, del lado más corto de dicho rectángulo, fluctúa entre:
A) 2 y 3
B) 5/2 y 3
C) 3 y 4
D) 3 y 5
E) 7/2 y 4
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
La cantidad de números de tres cifras que pueden formarse con los dígitos 1, 2, 4, 5, 6, 7 y 8, tal que dichos números sean impares, es:
A) 140
B) 147
C) 152
D) 160
E) 172
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 9 :
El costo del pasaje de Trujillo a Pacasmayo por el alza de combustible recientemente aumentó en una cantidad equivalente a la suma de los cuadrados de todos los números enteros que satisfacen la siguiente desigualdad:
|x²+1|² – 3|x²+1| – 4 < 0 ;
dicha cantidad es:
A) 2
B) 3
C) 4
D) 5
E) 6
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 10 :
Margarita guarda en su bolsillo monedas de 5 huaras, 2 huaras y 1 huara (huara es una moneda ficticia) por un monto de 33 huaras. Si en total hay doce monedas y cuatro de ellas son de 5 huaras, la probabilidad de que Margarita obtenga en su bolsillo dos monedas por un valor de 4 huaras es:
A) 5/33
B) 5/12
C) 5/132
D) 5/11
E) 4/33
RESOLUCIÓN :
Rpta. : "A"
