HABILIDAD LÓGICO MATEMÁTICO SOLUCIONARIO DE EXAMEN ADMISIÓN UNIVERSIDAD PRUEBA DE INGRESO CLAVES RESPUESTAS
PREGUNTA 16 :
Una familia de siete miembros está formada por los padres y sus cinco hijos, dos de los cuales son mayores de edad. Todos ellos deben ser vacunados. Para llegar al puesto de vacunación, deben cruzar un río; para ello cuentan con una canoa, pero esta solo puede soportar a dos adultos o a un adulto y dos menores de edad. Además, todos los adultos saben remar y los menores deben viajar acompañados siempre por algún adulto. ¿Cuántas veces, como mínimo, la canoa deberá cruzar el río para que todos los integrantes de la familia se vuelvan a reunir en el lugar de la partida inicial, luego de estar todos vacunados?
A) 5
B) 8
C) 6
D) 7
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 17 :
La figura representa una pieza de madera, en la cual se ha trazado líneas horizontales y verticales, con las cuales se ha determinado diez cuadrados congruentes cuyos lados miden 20 cm. Luego se traza dos diagonales y se escribe las letras S y M, como muestra la figura.
Si Aldo dispone de una sierra, ¿cuántos cortes rectos, como mínimo, realizará para obtener las partes triangulares
A) 4
B) 6
C) 7
D) 5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 18 :
Varios equipos participan en un torneo de fútbol y cada uno juega una sola vez con cada uno de los otros equipos. En cada partido, el equipo ganador recibe tres puntos; el que pierde, cero puntos y, si empatan, cada equipo recibe un punto. Si, al finalizar el torneo, la suma de los puntos de todos los equipos es 24 y la relación entre el total de partidos ganados con el total de partidos empatados es como 2 es a 3, ¿cuántos equipos jugaron el torneo?
A) 6
B) 5
C) 3
D) 4
RESOLUCIÓN :
• PP = PG = 2k
• PE 3k
Entonces: 3(2k) + 2(3k) = 24
⇒ k = 2
N° de partidos = 5k = 10
Luego:
n(n – 1)/2=10
⇒ n = 5 equipos
Rpta. : "B"
PREGUNTA 19 :
El punto central de una moneda de forma circular está ubicado en el punto C (– 3; 2) de un plano cartesiano XY. Tomando como eje de simetría a la recta de ecuación y = x, halle las coordenadas del punto simétrico del punto C.
A) (2; –5)
B) (–2; 3)
C) (2; –3)
D) (– 2; 5)
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 20 :
Dado el siguiente arreglo triangular, considerando igual distancia mínima de una letra a otra en cada lectura, indique de cuántas maneras diferentes se puede leer la palabra CAMINOS.
A) 87
B) 88
C) 89
D) 85
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 21 :
Luis sale a trabajar diariamente muy temprano, cuando su reloj indica la hora que se muestra en la figura. ¿A qué hora Luis sale al trabajo?
A) 3:37 a.m.
B) 3:36 a.m.
C) 3:38 a.m.
D) 3:39 a.m.
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 22 :
Si la hora exacta en este instante es 6h 47 min y si hace 63 horas que el reloj de Sara se adelanta 4 minutos cada 7 horas, ¿qué hora indica en este momento el reloj de Sara?
A) 7h 26 min
B) 7h 15 min
C) 7h 25 min
D) 7h 23 min
RESOLUCIÓN :
CRONOMETRÍA
Cada 7 horas se adelanta 4 min.
En 63 horas se habrá adelantado 36 min.
Si en este momento son las 6 h y 47 min
Entonces el reloj indicará: (6 h, 47 min + 36 min)
Las 7: 23
⇒ El reloj de Sara indica 7 h 23 min.
Rpta. : "D"
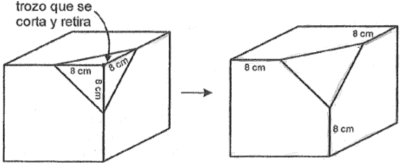
PREGUNTA 23 :
En el vértice de un cubo compacto de madera, cuyas aristas miden 16 cm, se corta y retira el trozo que tiene la forma de un tetraedro, como se indica en la figura. Si este proceso se realiza en todos los vértices del cubo, ¿cuántas aristas y cuántos vértices tiene el nuevo sólido obtenido, en ese orden?
A) 24; 24
B) 27; 12
C) 24; 12
D) 36; 18
RESOLUCIÓN :
En cada vértice se gana a 3 aristas, en consecuencia el cubo tendrá 24 aristas (las iniciales desaparecen).
En cada vértice se pierde dicho vértice, pero se genera 3 vértices, en consecuencia el cubo tendría 24 vértices pero cada vértice coincide con otras en cada arista, entonces habrá 24 − 32 = 12 vértices.
Por lo tanto: el cubo tendrá 24 aristas y 12 vértices.
Rpta. : "C"
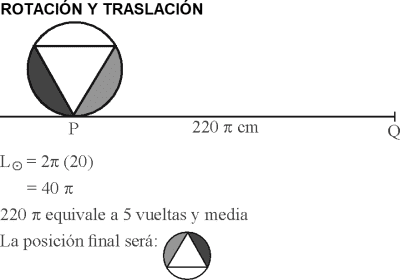
PREGUNTA 24 :
Una ficha circular, cuyo radio mide 20 cm, rueda sin deslizarse, a lo largo de una línea recta sobre una superficie plana, desde el punto P hasta el punto Q, como se muestra en la figura. La distancia entre los puntos P y Q es 220π cm. ¿Cómo se verá la ficha cuando llegue al punto Q?
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 25 :
La figura mostrada representa una estructura formada por alambres colocados en forma horizontal y vertical. ¿Cuántos cuadriláteros, en total, hay en la figura?
A) 59
B) 57
C) 65
D) 58
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 26 :
En una reunión a la que asisten \/arias personas, se sabe que, cada una de ellas, o bien dice siempre la verdad o bien miente siempre. Tres personas de esta reunión toman la palabra y dicen:
Persona 1:
− «Todos los presentes somos mentirosos».
− «Aquí no hay más de 9 personas».
Persona 2.
− «Entre los presentes, todos decimos la verdad».
− «Aquí hay más de 10 personas».
Persona 3.
− «Entre los presentes, hay exactamente cuatro mentirosos».
− «Aquí hay más de 8 personas».
Podemos afirmar que en la reunión hay
A) diez personas, de las cuales dos siempre mienten.
B) diez personas, de las cuales seis dicen siempre la verdad.
C) nueve personas, de las cuales cuatro mienten siempre.
D) diez personas, de las cuales, como máximo, tres siempre mienten.
RESOLUCIÓN :
VERDADES Y MENTIRAS
Persona 1: (F)
• Hay más de 9 personas Persona 2: (F)
• Hay 10 personas Persona 3: (V)
• Hay 4 mentirosos
• Hay más de 8 personas
Conclusión: Hay 10 personas de las cuales 6 dicen la verdad y 4 mienten.
Rpta. : "B"
PREGUNTA 27 :
A uno de los hijos varones de la familia Villanueva Castro se le pregunta: «¿Cuántos hermanos son ustedes?». Y él responde: «No somos más de 10 hermanos, y la cuarta parte de la cantidad de mis hermanos son varones. Además, la mitad de la cantidad de mis hermanos varones son médicos». Determine la cantidad de hijas que tienen les esposos Villanueva-Castro.
A) 7
B) 9
C) 6
D) 3
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 28 :
Juan tiene un terreno en forma de triángulo rectángulo cuyos catetos miden 40 m y 60 m. En este terreno, Juan quiere cercar una región rectangular R de área máxima, como se muestra en la figura. Determine el perímetro de la región R.
A) 140 m
B) 120 m
C) 90 m
D) 100 m
RESOLUCIÓN :
Rpta. : "D
PREGUNTA 29 :
Un vendedor tiene una balanza de dos platillos; pesas de 3 kg, 5 kg y 8 kg, dos de cada tipo, y más de 100 kg de arroz. Si un cliente le pide 49 kg de arroz, ¿cuántas pesadas, como mínimo, debe realizar el vendedor para atender el pedido?
A) 2
B) 3
C) 4
D) 5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 30 :
Escriba los números enteros desde el 4 al 15, sin repetirlos, en los cuadraditos de la figura de manera que la suma de los cuatro números escritos en cada lado del cuadrado grande sea la misma. ¿Cuál es el máximo valor de dicha suma?
A) 41
B) 42
C) 40
D) 43
RESOLUCIÓN :
Rpta. : "B"