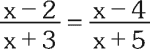ÁLGEBRA BECA 18 FORMULARIO CON EJEMPLOS RESUELTOS DEL TEMARIO PRONABEC PRUEBA UNICA NACIONAL PDF
PREGUNTA 1 :
Se tienen las funciones
Donde “d” y “c” son constantes, su punto de intersección es (– 2; –1).
Halla d+c.
A) – 1
B) – 2
C) 0
D) 1
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 2 :
Sea una función lineal, que pasa por los puntos: (– 1; 1) ∧ (4; 11). Indica su regla de correspondencia.
A) y=x+5
B) y= – 3x+1
C) y=2x+3
D) y=x+1
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 3 :
La edad de una persona hace 27 años es igual a la quinta parte de lo que tendría de aquí a 27 años despierto (sabiendo que duerme 8 horas diarias). Halla su edad hace 12 años.
A) 50
B) 51
C) 63
D) 60
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
Sea “m” el residuo de dividir
P(x)= x⁴ + 2x² + 1 entre Q(x)= x² – 1.
Halla el valor de R(m), siendo
A) 15
B) 16
C) 17
D) 18
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 :
Resuelve el siguiente sistema:
x + a ≥ 0
ax – 1 ≤ 0
siendo a<0
A) [ – a; ∞ [
B) [ 1/a ; − a ]
C) [ –a ; a ]
D) ] –∞ ; –a ]
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6 :
Sea el sistema:
ax + by = ab ... (1)
– bx + 2ay =– b² ... (2)
compatible determinada
Marca la alternativa correcta:
A) Se necesita el valor de “a” para conocer “x”
B) Se necesita el valor de “a” para conocer “y”
C) Se necesita el valor de “b” para conocer “x”
D) Se necesita el valor de “b” para conocer “y”
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 7 :
Al dividir
calcula 3Q(x) + R(x)
donde Q(x) es cociente y R(x) es residuo
A) 3x² + 6
B) 3x²
C) 3x² – 6
D) –6
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
Dada la siguiente función:
F(x)= 2x² – 4x – 1
Indica en qué cuadrante se encuentra ubicado el vértice de la gráfica de dicha función:
A) I cuadrante
B) II cuadrante
C) III cuadrante
D) IV cuadrante
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 9 :
Dada la ecuación de la recta:
Indica el valor de “a/m ” donde “m” es la pendiente de la recta y “a” es la abscisa en el origen.
A) 6p
B) – 4p
C) – 6p
D) – 8p
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 :
Sea F una función tal que x ∈ ℜ ; además, la función se define como “x” o uno menos.
Calcula.
A) –2
B) –1
C) 2
D) 1
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 11 :
Halla “x” en:
A) 3/2
B) 3/4
C) 2/3
D) 1
RESOLUCIÓN :
Ecuaciones exponenciales
Rpta. : "C"
PREGUNTA 12 :
Un grupo de profesores decide realizar un viaje, cuyos gastos ascienden a S/ 200. Días antes desisten de ir dos profesores por lo que cada profesor debe aportar S/ 5 más. ¿Cuántos profesores fueron de viaje?
A) 10
B) 8
C) 9
D) 7
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 13 :
Una familia paga S/.500 por 30 km de viaje, luego paga S/.700 por otros 45 km. Halla la ecuación lineal del costo por cada kilómetro recorrido.
A) y=x+100
B) y=40x + 50
C) y= 40x/3 + 100
D) y= x/3 + 100
RESOLUCIÓN :
Rpta. : "C"
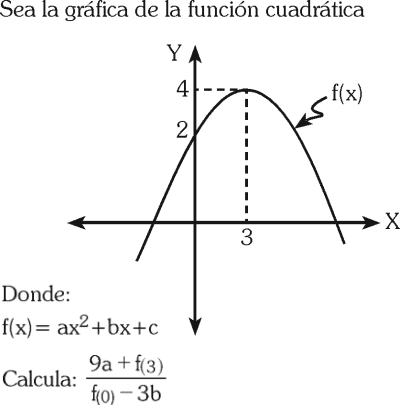
PREGUNTA 14 :
Sea la función cuadrática f(x)=ax² + bx + c de vértice v(p;p)
Si la función corta al eje “Y” en – p; p≠0
Halla el valor de “b”.
A) – p
B) 0
C) 2
D) 4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 15 :
Dada la función cuadrática:
f(x)=ax²+bx+6
f(x+1) – f(x– 1)=8(x+1)
Halla a+b
A) 2
B) 6
C) 8
D) 10
RESOLUCIÓN :
Funciones
Se observa:
f(x+1)=a(x+1)²+b(x+1)+6
f(x – 1)=a(x – 1)²+b(x – 1)+6
⇒ f(x+1) – f(x – 1)=a(4x)+2b=4ax+2b
∴ 4ax+2b ≡ 8x+8
→ a=2 ; b=4
∴ a+b=6
Rpta. : "B"
PREGUNTA 16 :
Resuelve la siguiente inecuación.
a(x+1) ≤ b(x+1); si a < b
A) [ 1;+∞[
B) ] – ∞ ; – 1 ]
C) [– 1;1]
D) [– 1;+∞[
RESOLUCIÓN :
Inecuaciones
De la inecuación
ax+a ≤ bx+b
⇒ a – b ≤ bx – ax
⇒ – (b – a) ≤ (b – a)x
como (b – a)>0
⇒ – 1 ≤ x
∴ “x”∈ [– 1;+∞[
Rpta. : "D"
PREGUNTA 17 :
La representación de la velocidad respecto al tiempo está dada por la siguiente función.
f(t)=– 5t²+40t – 8
Indica en qué tiempo la velocidad es máxima.
A) t=1
B) t=2
C) t=4
D) t=8
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 18 :
Al dividir P(x)=ax²+x+6 entre Q(x)=ax – 3a se obtuvo como resto 18.
Halla P(a+1).
A) 8
B) 6
C) 10
D) 12
RESOLUCIÓN :
División algebraica
Por teorema del resto:
ax – 3a=0 → x=3
R(x)=a(3)²+3+6=18 → a=1
⇒ P(x)=x²+x+6
⇒ P(2)=2²+2+6
Piden: P(1+1)
∴ P(2)=12
Rpta. : "D"
PREGUNTA 19 :
Dada la gráfica de una función cuadrática indica la regla de correspondencia.
A) 2x² – 4x+5
B) 2x²+ 4x+5
C) 2x² + 5
D) x² + 4x + 5
RESOLUCIÓN :
Función cuadrática
Del gráfico:
vértice: (1; 3)
(0; 5) ∈ f
Luego: f(x)=a(x – b)²+k
⇒ f(x)=a(x – 1)²+3
⇒ 5=a(x – 1)²+3 ⇒ a=2
∴ f(x)=2x² – 4x+5
Rpta. : "A"
PREGUNTA 20 :
Dadas las rectas:
x=2
y=3
3x – 2y=0
2x – 3y+5=0
indica en cuántos puntos se cortan las rectas.
A) Un solo punto
B) Dos puntos
C) Tres puntos
D) Cuatro puntos
RESOLUCIÓN :
Ecuación lineal
De las ecuaciones:
x=2 ∧ y=3
nótese que verifican las ecuaciones
3x – 2y=0 ∧ 2x – 3y+5=0 ⇒ x=2 ∧ y=3
Por lo tanto, estas rectas se cortan en un solo punto.
Rpta. : "A"
PREGUNTA 21 :
Dadas las siguientes proposiciones, ¿cuál de ellas nos representa a una función inyectiva?
A) La velocidad que marca el velocímetro de un automóvil
B) El número de DNI de una población
C) El tiempo de vida de un artefacto
D) La gráfica que describe el vuelo de un mosquito
RESOLUCIÓN :
Funciones
Dado que la función es inyectiva o uno a uno solo cumple la alternativa B, dado que cada persona se relaciona con su DNI.
Rpta. : "B"
PREGUNTA 22 :
A) –2
B) –1
C) 2
D) 1
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 23 :
Da la solución del siguiente sistema:
y ≥ – 1
x ≥ – 2
y ≤ x + 3
3x + 4y ≤ 0
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 24 :
El costo de un carro al inicio de un año es S/ 32 000, si tiene una devaluación de S/ 650 por cada año. Hallar el costo que tendrá dentro de 17 años.
A) S/ 20 900
B) S/ 25 900
C) S/ 29 950
D) S/ 20 950
RESOLUCIÓN :
Planteo de ecuaciones
Datos: Costo inicial=32 000
Devaluación=650 (por año)
Luego, para un tiempo de 17 años:
Costo final=32 000 – 650(17)
Costo final=S/ 20 950
Rpta. : "D"
PREGUNTA 25 :
Si f(0) = 1; f(1) = 0 ; f(– 1) = 6
Calcula f(2) siendo “f” una función cuadrática.
a) – 1
b) 2
c) 3
d) – 5
RESOLUCIÓN :
Funciones
Como “f” es cuadrática
f(x) = ax²+bx+c
Del dato
f(0) = 1 → c = 1 f(1) = 0
→ a+b+c = 0
a+b = – 1 ... (α)
f( – 1) = 6 → a – b+c=6
→ a – b=5 ... (β)
De “α” y “β”; a = 2 ∧ b = – 3
∴ f(x) = 2x² – 3x+1; luego, f(2) = 3.
Rpta. : "C"
PREGUNTA 26 :
A) – 7
B) – 3
C) 0
D) 3
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 27 :
A) 1
B) x
C) x³
D) x²
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 28 :
Siendo “f” una función lineal; además
f(2) = 0 ∧ f(1) = – 3, halla f(x).
a) f(x) = 3x+6
b) f(x) = – 3x+6
c) f(x) = – 3x
d) f(x) = 3x – 6
RESOLUCIÓN :
Funciones
Como “f” es lineal f(x) = ax+b.
Luego, del dato tenemos
x → f(2) = 2a+b → 2a+b = 0
x = 1 → f(1) = a+b → a+b = – 3
al resolver
a = 3 ∧ b = – 6
∴ f(x) = 3x – 6
Rpta. : "D"
PREGUNTA 29 :
Dos automóviles parten simultáneamente de un determinado punto. El primero recorre 10 km empleando una velocidad de 5 km/h; el segundo, utilizando el mismo tiempo que el primero, recorre 12 km a “y” km/h. Calcula “y”.
a) 5 km/h
b) 7 km/h
c) 6 km/h
d) 5,5 km/h
RESOLUCIÓN :
Planteo de ecuaciones
1°.
d = 10 km
v = 5 km/h
d = v.t
10 = 5t
t = 2 horas
2°.
d = 12 km
v = y
d = v.t
12 = y(2)
y = 6 km/h
Rpta. : "C"
PREGUNTA 30 :
a) 47
b) 48
c) 49
d) 50
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 31 :
Se tiene un rectángulo cuya área es 36 m² y su perímetro 30 m. Calcule la diferencia entre el mayor y menor de los lados.
A) 9
B) 10
C) 11
D) 12
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 32 :
Dado el polinomio
P(x;y) ≡ x³+y³+3(x²y+xy²)
Halle el valor de :
P(b −1;3 − b) − P(−1;1)
A) 1
B) 4
C) 8
D) 16
RESOLUCIÓN :
Polinomios Valor numérico Del polinomio
P(x;y) ≡ x³+y³+3x²y+3xy²
P(x;y) ≡ (x+y)³
Se pide P(b −1;3 − b) − P(−1;1)
= (b −1+3 −b)³−(−1+1)³
= 2³− 0=8
Rpta. : "B"
PREGUNTA 33 :
Al dividir el polinomio P(x) ≡ x⁴+1 entre el polinomio x² − 1, se obtiene un cociente Q(x) y residuo R(x). Calcule el equivalente de 3Q(x) − R(x).
A) 3x² − 2
B) 3x²+1
C) 3x²
D) 3x² −1
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 34 :
Factorice
P(a;b) ≡ 4 − a² − b²+2ab
A) (a+b+2)(a − b − 2)
B) (a − b+2)(b − a+2)
C) (a − b+2)(a+b − 2)
D) (a+b − 2)(b+a − 2)
RESOLUCIÓN :
Factorización Diferencia de cuadrados
P(a;b) ≡ 4 − (a² − 2ab+b²)
≡ 4 − (a − b)²
≡ (2+a − b)(2 − a+b)
Rpta. : "B"
PREGUNTA 35 :
De la igualdad
halle A+B+C.
A) − 3
B) − 2
C) 1
D) 3
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 36 :
Resuelva
A) CS={− 2}
B) CS={1}
C) CS={2}
D) CS={−1}
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 37 :
Un camión transporta 420 cajas. Al pasar por un controlador de peso este excedía el peso límite en 65 kg; al retirar 12 cajas el nuevo peso está 19 kg debajo del límite. Halle el peso de cada caja si todas pesan igual.
A) 10
B) 12
C) 9
D) 7
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 38 :
Las edades de tres hermanos son 15 ; 17 y 33 años. ¿Dentro de cuántos años la edad del mayor será igual a la suma de los otros dos hermanos?
A) 4
B) 3
C) 2
D) 1
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 39 :
Dada la ecuación cuadrática en “x”
2x²+3x+ a= 0
si el valor de una raíz es 1/2, calcule el valor de la otra raíz.
A) 1
B) −1/2
C) −2
D) −1
RESOLUCIÓN :
Ecuaciones de segundo grado
Teoremas de Cardano
Como una raíz de la ecuación es 1/2, considerando que la otra raíz sea “m”; calculamos la suma de raíces:
m + 1/2= −3/2
⇒ m = −2
∴ La otra raíz es −2.
Rpta. : "C"
PREGUNTA 40 :
Calcule la suma de valores de “x” en la ecuación
A) 5
B) 6
C) 7
D) 8
RESOLUCIÓN :
Ecuación de segundo grado
Teoremas de Cardano
De la ecuación
Tomamos
x² – 7x+4 = – 8
x² – 7x+12 = 0
Al factorizar luego los valores serán x₁=3; x₂=4; la suma es 7.
Rpta. : "C"
PREGUNTA 41 :
Evalúe | – 2x+3| cuando x<1
A) – 2x+3
B) 2x-3
C) – 2x – 3
D) 2x+3
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 42 :
Sea F(x) una función lineal en la cual se verifica:
• F(0) + F(1) = 3
• 3F(1) – F(0) = 13
Halle F( – 2).
A) 11
B) 12
C) –11
D) 13
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 43 :
Dada la función F definida por
F(x) = x+|x|
Indique su dominio y rango, respectivamente.
A) [0; +∞>; [0;+∞>
B) ] – ∞;+∞[; [0;+∞[
C) ] – ∞;+0]; [0;+∞[
D) ] – ∞;+∞[; ] – ∞;0]
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 44 :
Dada la función cuadrática F que corta al eje de las abscisas en los puntos (5;0) y ( – 1;0), halle el punto de corte con el eje de las ordenadas, sabiendo que el mínimo valor que toma la función es – 3.
A) (0;–1/3)
B) (0; –3/2)
C) (0;1/2)
D) (0;–5/3)
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 45 :
Simplifica
A) 15(x - 1)
B) 5(x²+x+1)
C) 15√(x² − 1)√(x² + x + 1 )
D) 15√(x − 1)√(x² − x + 1)
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 46 :
Factoriza
ab² – a³+a+b+a²b – b³
¿Cuál de los siguientes no es un factor?
A) 1 – a – b
B) a+b
C) 1 – a+b
D) 1+a – b
RESOLUCIÓN :
Factorización
Por agrupación y factor común , se tiene:
ab²+a²b+a+b – (a³+b³)
ab(a+b)+(a+b) – (a+b)(a² – ab+b²)
(a+b)[ab+1 – (a² – ab+b²)]
(a+b)(1 – a²+2ab – b²)
(a+b)[1 – (a² – 2ab+b²)]
(a+b)[1 – (a – b)²]
(a+b)(1 – a+b)(1+a – b)
No es un factor : 1 – a – b
Rpta. : "A"
PREGUNTA 47 :
Factoriza el siguiente polinomio.
(x+1)⁴+(x+2)³+(x+3)² – 7(x+1) – 5
A) (x+2)²(x²+4x+5)
B) (x+1)(x²+7x+3)
C) (x – 1)²(x²+5x+3)
D) (x+1)²(x²+3x+6)
RESOLUCIÓN :
Factorización
Criterio del aspa
Haciendo cambio de variable:
x+1→ a
a⁴+(a+1)³+(a+2)² – 7a – 5
a⁴+a³+3a²+3a+1+a²+4a+4 – 7a – 5
a⁴+a³+4a²
a²(a²+a+4)
Luego, reemplazamos “a” por x+1:
(x+1)²[(x+1)²+x+1+4]
(x+1)²(x²+2x+1+x+5)
(x+1)²(x²+3x+6)
Rpta. : "D"
PREGUNTA 48 :
Simplifica
A) – 2
B) 0
C) 1
D) 4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 49 :
Dado un polinomio P(x) de tercer grado con coeficientes enteros, tal que al dividir P(x)÷(x – b) se obtiene el siguiente esquema.
Calcula el valor de abc
A) – 18
B) – 15
C) – 12
D) – 9
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 50 :
Si la solución de la ecuación
es “m”, halla el valor de 6m+5.
A) 1
B) 2
C) 3
D) 4
RESOLUCIÓN :
Ecuaciones fraccionarias
Multiplicando en aspa tenemos:
(x - 2)(x+5)=(x+3)(x - 4)
⇒ x²+3x – 10 =x² – x – 12
⇒ 4x=–2
⇒ x=–1/2 ⇒ m –1/2
Luego: 6m+5=6(–1/2)+5=2
Rpta. : "B"
PREGUNTA 51 :
Resuelve
e indica la suma de soluciones.
A) – 1
B) –1/2
C) 1/2
D) 1
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 52 :
Un jardín de forma rectangular de 40 m de largo por 30 m de ancho está rodeado por un camino de arena uniforme. Halle la longitud del ancho de dicho camino si se sabe que su área es 296 m².
A) 2m
B) 3m
C) 4m
D) 4,5m
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 53 :
Resolver:
Indique el valor de: x+y
A) 0
B) 1
C) 2
D) 3
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 54 :
Dada la inecuación:
x² – Kx+9 < 0
Si su conjunto solución es:] 1;9 [ , indique el valor de "K"
A) 9
B) 12
C) 10
D) 13
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 55 :
Se conoce la siguiente función lineal:
f(x)=Ax+B
De modo que los pares ordenados (3;7), (a – 1; a – 1) y (a; a – 3) pertenecen a dicha función.
Halle A+B.
A) 10
B) 11
C) 12
D) 13
RESOLUCIÓN :
Fución lineal
Dada la función f(x)=Ax+B
Como (3;7)∈ f ⇒ 3A+B=7 ... (I)
(a – 1; a – 1)∈ f ⇒ (a – 1)A+B= a – 1 ... (II)
(a; a – 3)∈ f ⇒ aA+B= a – 3 ... (III)
De (II) y (III) se tiene: A= – 2
Luego; en (I): 3(– 2)+B=7
⇒ B=13
Finalmente: A+B=11
Rpta. : "B"
PREGUNTA 56 :
Dada la ecuación de la recta:
Indique el valor de a÷m donde "m" es la pendiente de la recta y "a" es la ordenada del punto de intersección con el eje "y".
A) 6p
B) – 6p
C) – 4p
D) – 8p
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 57 :
Siendo F una función lineal tal que (1;2) y (4;6) son coordenadas que pertenecen a la función F y G(x)=– 2x+3, calcule la suma de las pendientes de las funciones lineales F y G.
A) –1/3
B) – 2/3
C) 1/5
D) 1/3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 58 :
Se conoce el siguiente sistema:
Donde T y t están en segundos. Indique la región que representa dicho sistema.
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 59 :
Halle el residuo de la siguiente división:
A) 6x+5
B) 6x – 5
C) 5x – 6
D) 2x – 3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 60 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 61 :
Luego de resolver el siguiente sistema:
Halle el número de valores enteros del conjunto solución
A) 6
B) 7
C) 8
D) 9
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 62 :
Halle el rango de la función F: ℜ → ℜ, cuya regla de correspondencia es:
F(x)= – x²+4x
A) ] – ∞;+4]
B) [4; ∞[
C) ] – 4;+∞[
D) ] – ∞; – 4]
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 63 :
Dada la siguiente gráfica de la función “F”
¿Cuántas de las siguientes proposiciones son verdaderas?
I. El rango de f es [ – 3;3[
II. La pendiente de f es – 3 en el intervalo ]0;3[
III. f(8) – f( – 8)=0
A) Solo I
B) Solo II
C) Solo III
D) Ninguna
RESOLUCIÓN :
Funciones
I. (F), el rango es [ – 3;3]
II. (F), la recta está inclinada hacia la derecha en el intervalo ]0;3[ debe ser positiva
III. (F), f(8)=3 f( – 8)= – 3
⇒ f(8) – f( – 8)=6
Rpta. : "D"
PREGUNTA 64 :
Halle la ecuación de la recta cuya gráfica se da a continuación.
A) 2x+3y – 2=0
B) 2x+3y – 6=0
C) 2x-3y – 6=0
D) 6x+2y – 3=0
RESOLUCIÓN :
Funciones
Sea la ecuación: y=mx+b , donde b=2. Entonces, y=mx+2, luego reemplazando el punto (3;0) en la función, se tiene que x= – 2/3
Luego y= – 2/3x + 2
Que despejando es equivalente a 2x+3y – 6=0
Rpta. : "B"
PREGUNTA 65 :
Reducir la siguiente expresión:
Luego de como respuesta los dos tercios de E.
A) 19/13
B) 3/2
C) 13/19
D) 2/3
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 66 :
Sea
f(x)=a(x – h)² + k
cuya gráfica se da a continuación:
Hallar el valor de “a”.
A) 2
B) -2
C) – 3
D) 3
RESOLUCIÓN :
Funciones
Del gráfico; el vértice de la parábola es (1;2), entonces:
f(x)=a(x – 1)² + 2
Luego, (0 ;– 1) ∈ f , entonces:
– 1=a(0 – 1)² + 2⇒ a= – 3
Rpta. : "C"
PREGUNTA 67 :
Dada la siguiente gráfica:
Indicar cuál de las siguientes alternativas representa mejor la región sombreada:
A)
x – 3y + 9 ≥ 0
x – y + 1 ≤ 0
x ≥ 0 ; y ≥ 0
B)
x + 3y + 9 ≥ 0
x + y + 1 ≤ 0
x ≥ 0 ; y ≥ 0
C)
x + y + 9 ≥ 0
x – y + 1 ≤ 0
x ≥ 0 ; y ≥ 0
D)
x + 3y – 9 ≥ 0
x – y – 1 ≤ 0
x ≥ 0 ; y ≥ 0
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 68 :
Si “S” es el conjunto solución de la siguiente inecuación:
entonces se puede afirmar:
RESOLUCIÓN :
Rpta. : "D"
