DINÁMICA CIRCUNFERENCIAL PROBLEMAS RESUELTOS PREUNIVERSITARIOS
¿Qué es la dinámica circular?
Es una parte de la mecánica que estudia las condiciones que deben cumplir una o más fuerzas que actúan sobre un cuerpo, para que éste realice un movimiento circular.
Según la Segunda Ley de Newton la aceleración sobre un cuerpo se produce en la misma dirección y sentido que la fuerza resultante, esta aceleración cuando no es colineal con la velocidad produce en el móvil un movimiento curvilíneo.
Dado el movimiento curvilíneo, la aceleración lineal podrá descomponerse (proyectarse) en dos direcciones perpendiculares; normal y tangencial, generando las aceleraciones normal y tangencial.
Para resolver un problema de dinámica circunferencial, es decir, para analizar dinámicamente el movimiento de un cuerpo que se mueve describiendo una circunferencia, se sigue el siguiente procedimiento:
I) Identificar el centro de la circunferencia que le sirve de trayectoria.
II) Debido a que la fuerza resultante debe encontrarse en el plano que contiene a esta circunferencia, todas las fuerzas que no se encuentran en dicho plano de movimiento deben anularse.
III) Debemos identificar cuáles son las fuerzas radiales (fuerzas o componentes de fuerzas que se encuentran en la dirección del radio de la circunferencia en un instante dado).
IV) Teniendo en cuenta solo las fuerzas radiales, y considerando como positivas aquellas que apuntan hacia el centro y negativas las que se alejan del centro, se aplica la fórmula de definición de fuerza centrípeta (se elije una de las dos fórmulas).
Si es que hubieran fuerzas tangenciales (fuerzas o componentes de fuerzas que se encuentran en una dirección perpendicular al radio de la circunferencia en un instante dado), estas generarán una aceleración tangencial, que provocará un cambio en el módulo de la velocidad del cuerpo.
- CLIC AQUÍ Ver DINÁMICA LINEAL TEORÍA Y EJERCICIOS RESUELTOS PDF
- Ver DINÁMICA NIVEL BÁSICO
- Ver DINÁMICA CIRCULAR
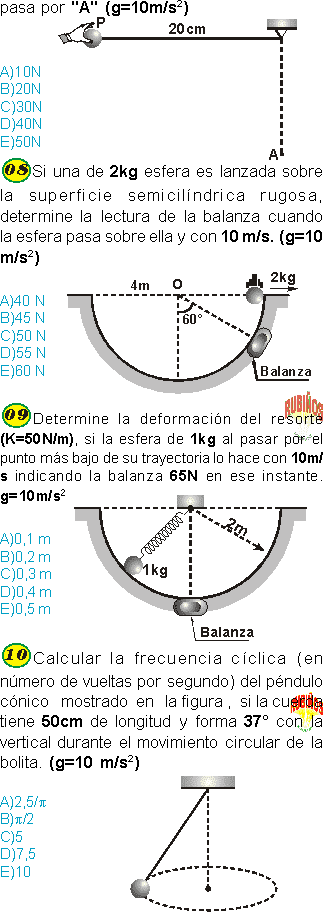
PREGUNTA 1 :
Amarrada a una cuerda de 5m una masa describe una trayectoria circular en un plano horizontal de manera que la cuerda siempre está formando 37° con la vertical. La velocidad angular con que gira la masa, en rad/s, es:
A) √5
B) √10
C) √10/2
D) √15
E) √7
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 2 :
Un cuerpo de 100 N, gira experimentando un MCU, con un radio de curvatura de 10 cm y una fuerza centrípeta de módulo 16 N. En estas condiciones, determine su rapidez angular en rad/s.
(g=10m/s²)
A) 1
B) 2
C) 3
D) 4
E) 5
Rpta. : "D"
PREGUNTA 3 :
Una esfera pequeña atada al extremo de una cuerda de 50 cm de longitud da vueltas a manera de un péndulo cónico. Si la cuerda forma 370 con la vertical en todo instante, ¿cuánto tardara la esfera en describir media circunferencia?
A) 𝛑/5 s
B) 2𝛑/5 s
C) 𝛑/3 s
D) 2𝛑/3 s
E) 𝛑/8 s
Rpta. : "A"
PREGUNTA 3 :
Se hace girar un balde lleno de agua en un plano vertical mediante una cuerda de 50 cm de longitud. ¿Cuál debe ser como mínimo, la velocidad en el punto más alto para que no caiga ni una gota de agua?
(g=10m/s²).
A) 2 m/s
B) √5 m/s
C) 5 m/s
D) 10 m/s
E) 2√5 m/s
Rpta. : "B"
PREGUNTA 5 :
Con respecto a las siguientes proposiciones, indique verdadero (V) o falso (F) según corresponda.
I. En un MCU la aceleración del móvil es constante.
II. En un movimiento circunferencial, el cuerpo tiende alejarse del centro de giro, debido a su inercia.
III. En un movimiento circunferencial, el cuerpo se mantiene a una misma distancia del centro de giro, debido a que la fuerza centrípeta y centrifuga se equilibran.
IV.
En un movimiento circunferencial la fuerza centrípeta es siempre la resultante total de totas las fuerzas que actúan sobre el cuerpo.
A) FVFV
B) FFVV
C) FVFF
D) VVVV
E) VFFF
Rpta. : "C"
PREGUNTA 6 :
Un motociclista se mueve en un plano horizontal describiendo una circunferencia de 30 m de radio. Si el coeficiente de rozamiento estático entre los neumáticos y la pista es 0,75; ¿cuál es la mayor rapidez que puede alcanzar la moto?
A) 10 m/s
B) 15 m/s
C) 12 m/s
D) 5 m/s
E) 7 m/s
Rpta. : "B"
Entonces, para que un cuerpo describa un movimiento circunferencial uniforme (M.C.U.), debe ser afectado por una fuerza resultante no nula dirigida hacia el centro de la circunferencia a la que denominamos fuerza centrípeta (Fcp), la misma que provoca una aceleración (dirigida hacia el centro de la trayectoria circunferencial) denominada aceleración centrípeta (acp).
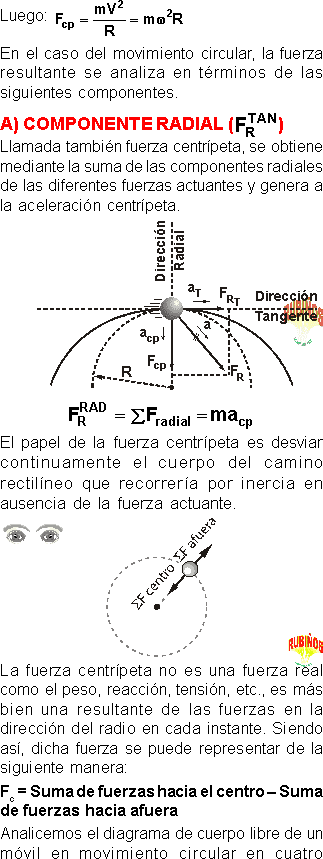
En el caso del movimiento circular, la fuerza resultante se analiza en términos de las siguientes componentes.
COMPONENTE RADIAL
Llamada también fuerza centrípeta, se obtiene mediante la suma de las componentes radiales de las diferentes fuerzas actuantes y genera a la aceleración centrípeta.
El papel de la fuerza centrípeta es desviar continuamente el cuerpo del camino rectilíneo que recorrería por inercia en ausencia de la fuerza actuante.
La fuerza centrípeta no es una fuerza real como el peso, reacción, tensión, etc., es más bien una resultante de las fuerzas en la dirección del radio en cada instante.
Siendo así, dicha fuerza se puede representar de la siguiente manera:
Fc = Suma de fuerzas hacia el centro – Suma de fuerzas hacia afuera
COMPONENTE TANGENCIAL
Ésta componente se obtiene sumando las componentes tangenciales de las diferentes fuerzas actuantes, produciendo la aceleración tangencial.
El papel de esta componente tangencial es la de modificar la velocidad, es decir acelera o retarda el movimiento.
I) En un movimiento rectilíneo no existe aceleración normal.
II) Los movimientos que carecen de aceleración tangencial se denominan uniformes.
III) En un movimiento circular la aceleración normal apunta hacia un centro estable.
En todo movimiento curvilíneo existe aceleración normal debido al cambio constante de la dirección de la velocidad.
IV) En todo momento el cuerpo esta sometido a la Fg la cual es la fuerza resultante que actúa sobre el cuerpo y apunta hacia el centro de la circunferencia, debido a ello se denomina "fuerza centrípeta".
V) Recordemos que (de la segunda ley de Newton) la fuerza resultante y la aceleración presentan igual dirección.
Para nuestro caso, la aceleración apunta hacia el centro de la circunferencia y se le denomina: "Aceleración centrípeta o normal".
La aceleración centrípeta no se encuentra a favor ni en contra de la velocidad, en consecuencia no mide "cambios en la rapidez".
La aceleración centrípeta mide de los cambios en la dirección de la velocidad.