ARITMÉTICA PREGUNTAS RESUELTAS ADMISIÓN UNIVERSIDAD SIMULACRO SOLUCIONARIO PRUEBA DE INGRESO DESARROLLADA 2023

PREGUNTA 1 :

El salario promedio de un trabajador era de S/1200; si se le hace un aumento de a% más S/300, recibiría un sueldo promedio de S/1680. Halle el valor de «a».

A) 15%

B) 10%

C) 35%

D) 25%

E) 45%

RESOLUCIÓN :

PROMEDIOS

Como a cada trabajador se le aumenta un a% más S/300

→ 1680=(100+a)%1200 +300

→ 1380=12(100 +a) → a=15

Rpta.: "A"

PREGUNTA 2 :

Si la razón de la suma con la diferencia de 2 números enteros positivos es 5/3, ¿cuál es el número mayor, si su producto es 64?

A) 24

B) 16

C) 32

D) 48

E) 64

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 3 :

Se tiene un aparato para mandar señales el cual tiene 5 focos y cuando se prenden unos y se apagan otros se forman señales diferentes. ¿Cuántas señales distintas se puede formar con dicho aparato?

A) 30

B) 31

C) 32

D) 33

E) 25

RESOLUCIÓN :

Análisis combinatorio – Principios de multiplicación

Cada foco tiene dos estados posibles, prendido o apagado.

Por tanto, por el principio de multiplicación, el número total de posibilidades para los 5 focos es : 2×2×2×2×2 = 2⁵ =32

Rpta.: "C"

PREGUNTA 4 :

En un salón de clase de 54 alumnos, 36 son varones. ¿Qué fracción son mujeres?

A) 1/3

B) 1/2

C) 1/4

D) 1/5

E) 2/3

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 5 :

Tres emisoras radiales transmiten una noticia cada 25 minutos, 20 minutos y 15 minutos, respectivamente. Si las emisoras transmiten simultáneamente la noticia hoy a las 8:00 a. m., ¿cuántas veces se transmitió la noticia simultáneamente en las tres emisoras entre las 9:00 a. m. y 11:30 p. m. del día de hoy?

A) 1

B) 2

C) 3

D) 4

E) 5

RESOLUCIÓN :

MCD – MCM – Aplicaciones

El intervalo de tiempo en el que las tres radios dan la noticia simultaneamente es:

MCM(25; 20; 15)=300 minutos <>5 horas.

Luego, desde las 8 a. m., las horas en que coinciden entre las 9:00 a. m. y 11:30 p. m. del mismo día son 1 p. m.; 6 p. m. y 11 p. m.

Rpta.: "C"

PREGUNTA 6 :

Se tiene dos grupos de 1100 libros de Álgebra y 1340 libros de Aritmética que se deben guardar en la menor cantidad de cajas en las cuales vayan la misma cantidad de libros. Si en cada caja se guardan libros de un mismo curso, ¿cuál es el mayor número de cajas de un mismo curso que se obtiene si no deben sobrar ni faltar libros?

A) 20

B) 55

C) 67

D) 122

E) 25

RESOLUCIÓN :

MCD – MCM – Aplicaciones

Si el número de cajas es mínimo, entonces el número de libros por caja es máximo; luego: Número de libros por caja=MCD(1100;1340)=20

Luego:

n.° de cajas de Álgebra= 1100÷20 =55

n.° de cajas de Aritmética= 1340÷20 =67

Rpta.: "C"

PREGUNTA 7 :

¿Cuántas parejas de números primos existen tales que su producto sea menor que 20?

A) 4

B) 5

C) 6

D) 7

E) 3

RESOLUCIÓN :

Números primos

Sean los números primos 2; 3; 5; 7...

Hallando las parejas de números primos cuyo producto es menor que 20:

2×3=6

2×5=10

2×7=14

3×5=15

Por tanto, existen 4 parejas.

Rpta.: "A"

PREGUNTA 8 :

Se reparte 738 en forma directamente proporcional a dos cantidades de modo que ellas están en la relación de 32 a 9. Calcula la suma de las cifras de la cantidad menor

A) 7

B) 11

C) 9

D) 8

E) 10

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 9 :

En un aula de clases, el 44 % de los alumnos tiene como media aritmética de sus notas el valor de 24. El 25 % de los alumnos restantes tiene como media aritmética un puntaje de 35. ¿Cuál debe ser la media aritmética de las notas de los alumnos restantes para que la media aritmética de todos los alumnos sea 31?

A) 32

B) 37

C) 41

D) 42

E) 40

RESOLUCIÓN :

Promedios – Media aritmética

Sean 100 alumnos

• 44 alumnos tienen MA=24

• 25 % 56=14 alumnos tienen MA=35

• 42 alumnos tienen MA=x

• 100 alumnos tienen MA=31

→ 44×24+14×35+42x=100×31 x=37

Rpta.: "B"

PREGUNTA 10 :

Una tienda comercial ofrece un descuento del 30% del precio de lista de cierto artículo, pero si se paga con tarjeta de crédito recibe un descuento adicional de 20%, pagando al final por el artículo 168 soles. El precio de lista del artículo, en soles, era de

A) 280

B) 320

C) 300

D) 350

E) 400

RESOLUCIÓN :

Se pide el precio de lista del artículo.

De los datos:

Del gráfico :168+14k+30k=100k

→ 168=56k

→ 3=k

Por lo tanto, el precio de lista es igual a 100k=S/300

Rpta.: "C"

PREGUNTA 11 :

Al precio de un artículo se le aumenta en a% y al nuevo precio se le disminuye en un

(100 – a) %. Si el precio final es de 96% del precio inicial, entonces el valor de a es:

A) 60

B) 50

C) 70

D) 80

E) 85

RESOLUCIÓN :

Sea P el precio inicial.

Rpta.: "A"

PREGUNTA 12 :

Si la media armónica de dos números enteros es a la media geométrica al cuadrado como 2 es a 5, entonces la media aritmética de los dos números enteros es

A) 2,3

B) 2,5

C) 2

D) 2,8

E) 2,7

RESOLUCIÓN :

Promedios

Sean A y B los dos números enteros.

Por dato

Rpta.: "B"

PREGUNTA 13 :

Al multiplicar N por 27 su número de divisores aumenta en 90. Si N=16×5^a, entonces el valor de a es

A) 5

B) 2

C) 4

D) 5

E) 6

RESOLUCIÓN :

TEMA : Números primos y compuestos

Se tiene :

Rpta.: "A"

PREGUNTA 14 :

20 obreros se comprometen a hacer una obra en 20 días trabajando 8 horas diarias. Después de 12 días de trabajo, se acordó que la obra quedaría terminada en 4 días antes del plazo estipulado y así se hizo. El número de obreros adicionales que se contrataron teniendo en cuenta que se aumentó 2 horas de trabajo diario es

A) 32

B) 28

C) 22

D) 18

E) 12

RESOLUCIÓN :

TEMA : Magnitudes

Se pide el número de obreros adicionales.

De los datos

PREGUNTA 15 :

Dos números están en la relación de 2 a 7; agregando a uno de ellos 73 y 138 al otro, se obtienen cantidades iguales. Halla el menor número.

A) 52

B) 26

C) 117

D) 13

E) 91

RESOLUCIÓN :

RAZONES Y PROPORCIONES

Piden el menor de los dos números.

Sean A y B los números, entonces A=2k ; B=7k

Por condición A+138=B+73

⇒2k+138=7k+73 ⇒ 5k=65 ⇒ k=13

Finalmente, hallamos el menor: 2k=26

Por lo tanto, el menor número es 26

Rpta. : "B"

PREGUNTA 16 :

Patricia quiere comprar un artefacto y el vendedor le ofrece un descuento del 10% y un descuento adicional del 20 % por tener la tarjeta de la tienda. ¿Cuál es el descuento total que le ofrece a Patricia?

A) 28%

B) 30%

C) 29%

D) 25%

E) 26%

RESOLUCIÓN :

TEMA : Regla del tanto por ciento

A Patricia le hacen dos descuentos sucesivos del 10% y 20 %. Hallaremos el descuento equivalente.

Deq=100% – (100% – 10%)(100% – 20%)

Deq=100% – 9 0 % × 8 0%

Deq=100% – 72% =28%

Rpta. : "A"

PREGUNTA 17 :

Calcula el MCD de dos números sabiendo que el producto es 4 860 y el MCM es 270.

A) 9

B) 16

C) 15

D) 12

E) 18

RESOLUCIÓN :

Máximo común divisor - Mínimo común múltiplo

Piden el MCD de dos números.

Sean A y B los números.

Por propiedad, se cumple que: A×B=MCD(A;B)×MCM(A;B)

Entonces: 4860=MCD(A; B) ×270

⇒ MCD(A; B) =18

Rpta. : "E"

PREGUNTA 18 :

Luis desea obtener en 5 años S/50 000. Si la institución financiera le paga una tasa del 12% simple anual, ¿cuánto debe depositar hoy para recibir ese monto en los 5 años?

A) S/25 000

B) S/31 250

C) S/33 150

D) S/28 250

E) S/31 250

RESOLUCIÓN :

TEMA : Regla de interés

Del enunciado, sabemos que Luis desea obtener un monto de S/50 000, y tenemos los siguientes datos:

Capital: N

Tasa: 12% anual

Tiempo: 5 años

Sabemos que M=C+ I M=C+C× r%×T

Reemplazando los datos, obtenemos

50 000=N+N×12%5

50 000=160%N

∴ 31 250=N

Rpta.: B

PREGUNTA 19 :

En una elección, una moción fue aprobada por una votación de 5 a 3, según esto, diga qué parte de los votantes estaban a favor.

A) 5/9

B) 5/7

C) 5/11

D) 5/8

E) 5/6

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 20 :

Identifica la alternativa cuya operación entre conjuntos representa el área de la región sombreada.

a) (A ∪ B) ∪ C

b) (A ∩ B) – C

c) (A ∪ B) ∩ C

d) (A Δ B) ∩ C

e) (A ∪ C) ∩ B

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 21 :

Se invierte un capital de S/30 000 en un proyecto que paga el 5% anual, ¿cuál es el interés simple generado si el proyecto tuvo una vida útil de 2 años y medio?

A) 4000

B) 4500

C) 3750

D) 3500

E) 3720

RESOLUCIÓN :

TEMA: Regla de interés

Del enunciado se tienen los datos

C=S/30 000

r%=5% anual

T= 2,5 años

Piden el interés simple generado.

Sabemos que I=C×r%×T

Reemplazamos los datos.

I = 30000 × 5% × 2,5

I =300×12,5

∴ I =3750

Rpta.: C

PREGUNTA 22 :

Si 45 es la cuarta diferencial de a, b y c; además, 140 es la tercera diferencial de 2a y 160. Halla la media aritmética de b y c.

A) 64,0

B) 66,0

C) 62,0

D) 63,5

E) 67,5

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 23 :

A) 52

B) 42

C) 49

D) 40

E) 50

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 24 :

Tres socios aportan 1000, 1500 y 2000 soles respectivamente para la formación de una empresa. Al cabo de cierto tiempo, obtienen un beneficio de 4500 soles. ¿Cuánto ganó el que aportó menor capital?

a) 1000 soles

b) 1250 soles

c) 900 soles

d) 1200 soles

e) 500 soles

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 25 :

Si la expresión

es irreductible, determina el valor de N.

A) 3/7

B) 1/7

C) 3/8

D) 1/16

E) 3/16

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 26 :

En un colegio, el 60% aprobó Aritmética, el 32% aprobó Álgebra y los que aprobaron Aritmética y Álgebra representan el 60% de los que no aprobaron ninguno de los dos cursos. Si 42 aprobaron Aritmética y Álgebra. Calcula el número de alumnos de dicho colegio.

a) 330

b) 340

c) 350

d) 345

e) 335

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 27 :

Si el complemento aritmético (CA) de un numeral capicúa de cuatro cifras es 771, indica la cifra de decenas del capicúa.

a) 3

b) 1

c) 2

d) 4

e) 5

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 28 :

Halla el valor nominal de una letra que vence el 23 de abril y descontada el 24 de marzo al 4% del mismo año, se disminuye en 30 soles.

a) 10000 soles

b) 7000 soles

c) 6600 soles

d) 9000 soles

e) 8000 soles

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 29 :

Halla el mayor de dos números tales que su máximo común divisor sea 36 y su mínimo común múltiplo sea 5148.

A) 368

B) 428

C) 468

D) 398

E) 488

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 30 :

Determina la cantidad de divisores de 4320 que tienen raíz cuadrada exacta.

A) 6

B) 3

C) 5

D) 4

E) 7

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 31 :

Halla el menor múltiplo de 15 tal que la suma de su tercera parte y séptima parte es un cuadrado perfecto.

A) 195

B) 165

C) 180

D) 215

E) 210

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 32 :

Dada la siguiente sucesión: 1; 2; 3; 4; ... ....; 900. ¿Cuántos no son múltiplos de 3 ni de 5 ?

A) 480

B) 180

C) 420

D) 900

E) 300

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 33 :

A un teatro asisten muchas personas, se sabe que de cada cinco varones que entran, tres entran con un niño y de cada siete mujeres, cuatro entran con un niño. Además, por cada seis varones entran cinco mujeres, si entraron 678 niños en total, ¿cuántos adultos entraron al teatro?

a) 1105

b) 1135

c) 1065

d) 1050

e) 1155

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 34 :

Una fábrica de jabones requiere empaquetar barras de jabón, cuyas dimensiones son: 8 cm, 15 cm y 20 cm, en cajas cúbicas del menor tamaño posible, para luego ser transportadas en un camión cuya tolva es de 10,80m×6m×3,6m. ¿Cuántos jabones será posible transportar en dicho camión?

a) 720

b) 97200

c) 97620

d) 97720

e) 9720

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 35 :

Un jugador de billar A le da ventaja a otro B, 40 carambolas para 100 y B le da ventaja a otro C, 60 carambolas para 100. ¿Cuántas carambolas de ventaja debe dar A a C en un juego de 100?

A) 64

B) 72

C) 76

D) 68

E) 74

RESOLUCIÓN :

Rpta. : "C"

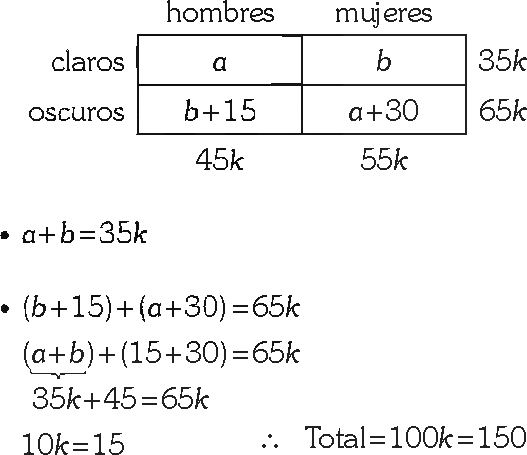
PREGUNTA 36 :

A una reunión asiste cierto número de personas; se observa que el 45 % son hombres y el resto mujeres, el 35 % de los asistentes tiene ojos claros y el resto oscuros. Si la diferencia entre mujeres con ojos oscuros y hombres con ojos claros es 30 y la diferencia entre hombres con ojos oscuros y mujeres con ojos claros es 15; el total de personas que asistió a la reunión, fue:

A) 125

B) 135

C) 140

D) 150

E) 160

RESOLUCIÓN :

TEMA : Tanto por ciento

Se pide el total de personas.

De los datos