RM SAN MARCOS SOLUCIONES DE ADMISIÓN

PREGUNTA 16 :

En el siguiente arreglo numérico, el número en cada círculo es la suma de los números que se encuentran en los dos círculos inmediatamente inferiores y unidos a este por un segmento de recta. ¿Cuál es la suma de los números en los círculos sombreados?

A) 40

B) 120

C) 140

D) 60

E) 240

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 17 :

Sobre un papel y usando un lápiz, Jorge realizó el esbozo de una ventana, donde ABEF y BCDE son rectángulos, como se observa en la figura. ¿Cuál es la longitud mínima recorrida por la punta de su lápiz al hacer el esbozo de la ventana?

A) 7,58 m

B) 8,06 m

C) 8,36 m

D) 7,86 m

E) 8,18 m

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 18 :

Determine, en la figura, el número total de triángulos.

A) 30

B) 26

C) 28

D) 29

E) 27

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 19 :

Vicky tiene una balanza de dos platillos y una colección de pesas de 1 g, 10 g, 100 g y 1000 g. Si desea pesar con dicha balanza 5659 g de maní confitado en una sola pesada y, además, su colección consta de diez pesas de cada tipo, ¿cuántas pesas de su colección, como mínimo, debe usar.

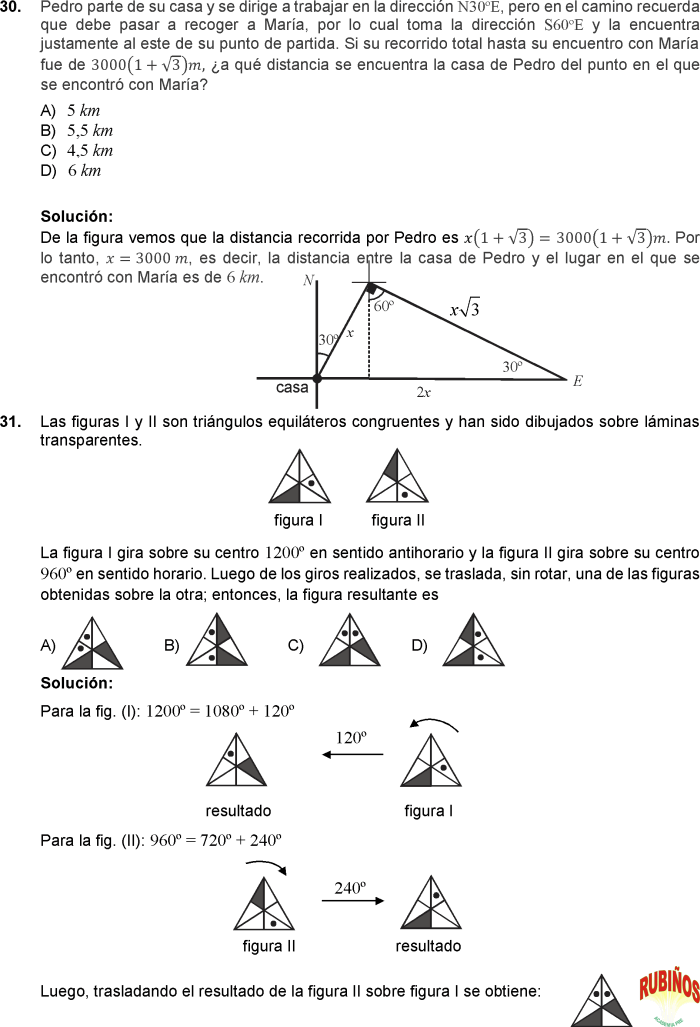
A) 20

B) 17

C) 14

D) 13

E) 25

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 20 :

La figura muestra las vistas frontal, perfil derecho y horizontal de un sólido de volumen máximo. Halle el número de vértices de dicho sólido.

A) 20

B) 21

C) 23

D) 22

E) 19

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 21 :

En el siguiente diagrama de flujo, determine el valor de M que se imprime al final del proceso.

A) 27

B) 33

C) 31

D) 35

E) 29

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 22 :

María y José nacieron el 14 de febrero de 2000. Se conocieron el 14 de febrero de 2020, se enamoraron y decidieron contraer matrimonio exactamente 212 días después de que cumplan 30 años de edad.

¿En qué fecha y día de la semana se realizará la boda?

A) Sábado 7 de setiembre de 2030

B) Sábado 21 de setiembre de 2030

C) Miércoles 13 de setiembre de 2030

D) Sábado 14 de setiembre de 2030

E) Miércoles 20 de setiembre de 2030

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 23 :

En la figura, recorriendo solo por las líneas, ¿cuántas rutas diferentes existen para ir desde el punto A hasta el punto B si solo se puede seguir las direcciones dadas por las flechas?

A) 352

B) 342

C) 234

D) 294

E) 362

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 24 :

María estaba segura de que uno de sus cinco hijos se había comido el pastel que ella había comprado para su abuelito. Cuando preguntó a cada uno de los niños, sobre quién se había comido el pastel, obtuvo las siguientes respuestas:

• Angélica: "Yo no fui".

• Benito: "Angélica miente".

• Isabel: "Yo fui".

• Luz: "Benito se lo comió".

• Miguel: "Yo no fui".

Si solo uno se comió el pastel y solo una de las afirmaciones es verdadera, ¿quién se comió el pastel?

A) Isabel

B) Benito

C) Luz

D) Miguel

E) Angélica

RESOLUCIÓN :

De los enunciados, asumimos un culpable y que luego cumpla la condición de solo un enunciado verdadero.

Rpta. : "D"

PREGUNTA 25 :

Manuel tiene un recipiente sin marcas que le facilite hacer mediciones. El recipiente fue llenado con 25 litros de leche. Además, tiene otros dos recipientes vacíos sin graduar: uno de 11 litros y otro de 8 litros de capacidad. Sin desperdiciar leche, ¿cuántos trasvases debe realizar Manuel, como mínimo, para tener 5 litros en uno de los recipientes?

A) 4

B) 3

C) 5

D) 6

E) 7

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 26 :

En el siguiente arreglo de letras considerando igual distancia mínima de una letra a la otra en cada lectura, ¿de cuántas maneras distintas se puede leer ozono?

A) 18

B) 52

C) 56

D) 36

E) 54

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 27 :

En un tablero de madera de forma hexagonal, se han dibujado diez triángulos equiláteros congruentes, tal como muestra la figura. La longitud de los lados de estos triángulos equiláteros es 30 cm. Si se dispone de una sierra que puede cortar, a lo más, 60 cm de longitud, ¿cuál es el mínimo número de cortes rectos que se deben realizar para separar los diez triángulos?

A) 5

B) 3

C) 6

D) 4

E) 2

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 28 :

La figura representa un parque en forma rectangular y la región triangular TUV representa la base de una estatua (P, Q, R, S, T, U, V son puntos medios). ¿Qué parte del área total del parque constituye el área de la base de la estatua?

A) 1/48

B) 1/40

C) 1/24

D) 1/30

E) 1/60

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 29 :

En el sistema de poleas que se muestra, si el bloque M sube 60cm, ¿cuánto baja el bloque N?

A) 100 cm

B) 120 cm

C) 90 cm

D) 140 cm

E) 80 cm

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 30 :

En el siguiente arreglo numérico triangular, halle la suma de los elementos de la fila F₁₅.

A) 19 450

B) 14 950

C) 45 190

D) 41 950

E) 49 150

RESOLUCIÓN :

Rpta. : "D"

SEGUNDA PRUEBA

PREGUNTA 1 :

María visitó un orfanato y regaló un juguete diferente a cuatro niños: una bicicleta, un carrito, una patineta y una pelota, y ningún niño recibió mas de un regalo. Respecto del regalo recibido, cada niño dijo:

Angel: «Yo recibí una pelota».

Luis: «Yo recibí un carrito».

Leandro: «Angel recibió una bicicleta».

Isidro: «Yo recibí una bicicleta».

Si solo uno de ellos miente y los otros tres dicen la verdad, ¿qué juguete recibió Leandro?

A) Pelota

B) Bicicleta

C) Carrito

D) Patineta

PREGUNTA 2 :

Los amigos Rubén, Horacio, Marcos, Carlos, Jorge y Teodoro participan en una maratón y llevan en sus respectivas camisetas los números 107, 101, 109, 119, 103 y 113. Un periodista deportivo narró la llegada a la meta de los amigos: «El 107 llego antes que el 101 y después que el 109», «El 109 llegó después que el 119 y este después que el 113» y «El 103 fue el último en cruzar la meta».

¿Cuál de los amigos llegó en cuarto lugar?

A) Carlos

B) Rubén

C) Marcos

D) Horacio

PREGUNTA 3 :

En dos caras de un cubo se tiene un punto, y en las otras se han distribuido dos, tres, cuatro y cinco puntos, de tal modo que el cubo puede visualizarse como se muestra a continuación:

¿Qué cantidad de puntos hay en la cara X, si en la cara Y hay la mayor cantidad de puntos posible?

A) 4

B) 5

C) 1

D) 2

PREGUNTA 4 :

Tres enfermeros acompañados de dos niños guía se encuentran en la orilla de un río que deben cruzar para llegar a la aldea donde los esperan. Disponen de una canoa en la cual pueden viajar remando, hasta dos niños o un enfermero, pero no un niño y un enfermero juntos (los cinco saben remar). ¿Cuántas veces, como mínimo, la canoa debe cruzar el río para asegurar el paso de los tres enfermeros?

A) 11

B) 10

C) 12

D) 9

PREGUNTA 5 :

Si Javier no es mayor que Alberto, Luis no es mayor que Javier, César no es menor que Javier y todos tienen diferentes edades, ¿quién es el menor de todos?

A) Cesar

B) Alberto

C) Luis

D) Javier

PREGUNTA 6 :

La figura representa una plancha de madera en la que se observan siete cuadrados congruentes ¿Cuántos cortes rectos, como mínimo, se debe realizar con una sierra eléctrica para separar los siete cuadrados?

A) 4

B) 3

C) 7

D) 5

PREGUNTA 7 :

Elena tiene cinco pares de zapatillas blancas y cuatro pares de zapatillas grises en una caja. ¿Cuántas zapatillas debe extraer al azar, como mínimo, para tener con certeza un par de zapatillas blancas que pueda usar?

A) 14

B) 13

C) 15

D) 16

PREGUNTA 8 :

Se tiene una hoja de papel de forma cuadrada cuyos lados miden 20 cm, tal como se indica en la figura. A esta hoja de papel se le hacen cuatro cortes paralelos a las diagonales del cuadrado, tal como se muestra en la figura. Si las longitudes de los cuatro cortes suman 16√2 cm, ¿cuál es el perímetro del trozo de papel octogonal obtenido?

A) 16( √2 + 2) cm

B) 16( √2 + 1) cm

C) 16( √2 +1) cm

D) 32( √2 +3) cm

PREGUNTA 9 :

La figura representa una estructura que tiene la forma de un tronco de pirámide. ¿De cuántas maneras diferentes se puede ir desde el punto A hasta el punto G sin pasar más de una vez por un mismo vértice, recorriendo solo los segmentos que muestra la figura y sin, pasar por el punto H?

A) 9

B) 12

C) 10

D) 11

PREGUNTA 10 :

En una casa de antigüedades, un reloj se atrasa cuatro minutos cada cinco horas. Este reloj se pone a la hora exacta al mediodía y se le pondrá nuevamente a la hora exacta a las 8:00 a. m. del día siguiente. ¿Cuántos minutos se debe adelantar para que marque la hora exacta?

A) 18

B) 20

C) 12

D) 16

PREGUNTA 11:

La figura representa una estructura construida con alambre. La longitud de los lados de cada uno de los cuadrados pequeños mide 1 cm. Si una hormiga se encuentra en el punto P, ¿cuál es la longitud mínima que debe recorrer la hormiga para pasar por toda la estructura y terminar en el punto Q?

A) 29 cm

B) 27 cm

C) 30 cm

D) 28 cm

PREGUNTA 12 :

Las canciones M, N, P, Q y R están sonando seguidas, en ese orden, ininterrumpidamente. Es decir, cuando la M termina, empieza la N; cuando la N termina, empieza la P; cuando la P termina, empieza la Q; cuando la Q termina, empieza la R, y cuando termina la R, comienza de nuevo la M, etc. La canción M dura 3 min 20 s; la N, 2 min 30 s; la P, 2 min; la Q, 1 min 40 s y la R, 4 min. Qori sale de casa justo cuando lleva sonando 50 segundos la canción Q. Si Qori vuelve a casa exactamente una hora y media más tarde, ¿qué canción estará sonando?

A) R

B) P

C) N

D) M

PREGUNTA 13:

Un cuadrado mágico multiplicativo es aquel cuyo producto de los tres elementos de cada fila, columna o diagonal es siempre el mismo. Complete los recuadros de la figura, escribiendo números enteros para que resulte un cuadrado mágico multiplicativo y obtenga la suma de los números con que se completa dicho cuadrado.

A) −18

B) −26

C) −8

D) −6

PREGUNTA 14 :

En un campo abierto, dos cuatrimotos A y B parten al mismo tiempo de un mismo lugar con trayectorias perpendiculares, siguiendo el recorrido que se detalla y luego se detienen. La cuatrimoto A recorre 12 km en la dirección norte, luego recorre 6√2 km en dirección NE y, finalmente, 12√3 km en la dirección este. La cuatrimoto B recorre 6 km en la dirección este y luego recorre 24 km en dirección N60°E. Al detenerse, ¿a qué distancia de la cuatrimoto A se encuentra la cuatrirnoto B?

A) 6 km

B) 6√3 km

C) 12 km

D) 3√3 km

PREGUNTA 15 :

El 28 de julio de 2021, el Perú celebrará 200 años de la proclamación de la Independencia. Si el 1 de enero de 2018 fue lunes, ¿qué día se celebrará el bicentenario de la Independencia del Perú?

A) Lunes

B) Martes

C) Miércoles

D) Jueves

CLAVES DE RM : 1)D 2)B 3)D 4)D 5)C 6)A 7)A 8)D 9)D 10)D 11)A 12)C 13)D 14)A 15)C

SOLUCIONARIO

RM SAN MARCOS SOLUCIONES DE ADMISIÓN

Bruno montes