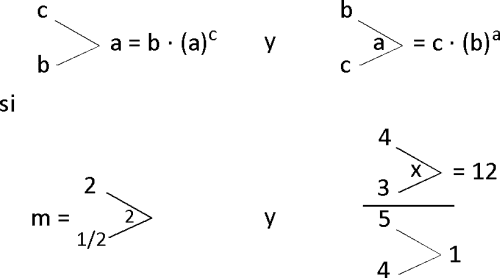RAZONAMIENTO MATEMÁTICO UNI DE EXAMEN DE ADMISIÓN UNIVERSIDAD DE INGENIERÍA SOLUCIONADO

PREGUNTA 1: 
En R definimos la operación matemática representada por * mediante 
Determine el valor de 1* 3. 
A) 1 
B) 2 
C) 3 
D) 4 
E) 5 
RESOLUCIÓN : 
Rpta. : "D"
PREGUNTA 2: 
Establezca el elemento que continúa a la sucesión. 

RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3: 
¿Cuál de las alternativas muestra el correcto despliegue? 

RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4: 
Encuentre la figura que sigue en la sucesión
RESOLUCIÓN :
Al analizar las figuras mostradas y la ley de formación que presentan, observamos lo siguiente: 
– Los nombres empiezan a bajar de línea en línea. 
– Los números empiezan a subir de línea en línea.
– La cantidad de letras que conforman los nombres es igual a la suma de los dos números. 
En consecuencia la alternativa correcta es
Rpta. : "D"
PREGUNTA 5: 
Dadas las siguientes proposiciones verdaderas: 
1. Todos los peluches son rellenados con lana. 
2. Existen peluches osos y peluches tigres. 
3. Algunas sillas son rellenadas con lana. 
¿Cuáles de las siguientes oraciones son verdaderas o falsas? 
I. Solo las sillas de niños son rellenadas con lana. 
II. Todos los peluches tigres están rellenados con lana. 
III. Los peluches monos no están rellenos con lana. 
A) FFV 
B) FVF 
C) VVV 
D) FFF 
E) VVF 
RESOLUCIÓN :
Tema: Razonamiento lógico 
I. Solo las sillas de niños son rellanadas con lana es falsa, puesto que de la proposición 3, no se especifica el tipo de silla. 
II. Todos los peluches tigres están rellanadas con lana es verdadera, esto se obtiene de la proposición 1. 
III. Los peluches monos no están rellanos con lana es falsa, esto se obtiene de la proposición 1.
Rpta. : "B"
PREGUNTA 6: 
Simplifique la proposición siguiente: 
[(∼p ∨ q)∧(~ q ∨ r)] → (∼ r ∨ p) 
A) p ∨ ∼r  
B) q 
C) r 
D) p
E) p ∨ q ∨ r 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 7: 
Si la proposición 
(p ∨ ∼ r) ↔ (s → w) es verdadera 
y (∼ w) → (∼ s) es falsa, 
halle el valor de verdad de las proposiciones. 
I. (p ∧ q) ∨ (r ∨ s) 
II. (s ↔ ∼ w) → (r ∧ ∼ p) 
III. [t → (w ∨ ∼ p)] ∧ ∼ (p → r) 
A) VVV 
B) VVF 
C) FFF 
D) VFF 
E) FFV 
RESOLUCIÓN :
Tema: Lógica proposicional 
Rpta. : "B"
PREGUNTA 8: 
Una familia consta de dos padres, dos madres, cuatro hijos en total, dos hermanos, una hermana, un abuelo, una abuela, dos nietos, una nieta, dos esposos, una nuera. ¿Cuántas personas como mínimo conforman dicha familia? 
A) 6 
B) 7 
C) 8 
D) 9 
E) 10 
RESOLUCIÓN :
Tema: Situaciones lógicas 
Rpta. : "B"
PREGUNTA 9: 
Los obreros A, B, C y D hacen una misma obra por sí solos en 20, 30, 40 y 25 días respectivamente. Empiezan el trabajo los obreros A y B, luego de 3 días se retira B y entra C que trabaja junto con A durante 2 días. Al término de los mismos se retira C e ingresa D y junto con A terminan la obra. ¿Cuántos días tienen que trabajar A y D para terminar la obra? 
A) 6 
B) 20/3 
C) 15/2 
D) 17/2 
E) 9 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10: 
Se tiene 20 bolillas numeradas de 1 al 20. ¿Cuál es el menor número de bolillas que se deben extraer para estar seguro de haber obtenido por lo menos 2 bolillas cuya suma sea 21? 
A) 5 
B) 10 
C) 11 
D) 12 
E) 15 
RESOLUCIÓN :
Tema: Certezas 
De la información brindada, obtenemos:
– Nos piden 2 bolillas que sumen 21. 
– La peor situación que puede ocurrir es extraer las bolillas numeradas del 11 al 20, es decir 10 bolillas. 
Luego, extraer cualquier bolilla de las restantes, con seguridad obtendremos dos bolillas que sumen 21, entonces 10 + 1 = 11 es el menor número de bolillas que debemos extraer. 
Rpta. : "C"
PREGUNTA 11: 
Si x(x – 3) = –1, halle el valor de x³.x³ – 18x³+5 
A) –1 
B) 2 
C) 3 
D) 4 
E) 5 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 12: 
Entre las alternativas presentadas, ¿qué figura en transparencia resulta de rotar y superponer el siguiente par? 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 13: 
Una persona sube una escalera de tal manera que por cada 8 gradas que sube, baja 3. Si recorrió en total 173 gradas, ¿cuántas gradas en total descendió? 
A) 34 
B) 38 
C) 45 
D) 48 
E) 50 
RESOLUCIÓN :
En cada operación sube 8 y baja 3, cuando solo le falta por subir 8 gradas, ya subió la escalera y, por lo tanto, ya no bajará. 
Supongamos que realizó “x” operaciones antes de subir las últimas 8 gradas. 
8x + 3x + 8 = 173 
→ x = 15
 Descendió 2(15) = 45 gradas. 
Rpta. : "C"
PREGUNTA 14: 
¿Cuál es el valor de x? 
A) 5 
B) 6 
C) 7 
D) 8 
E) 9 
RESOLUCIÓN :

Rpta. : "C"
PREGUNTA 15: 
En la figura, halle el valor de X+ Y – Z 
A) 18 
B) 21 
C) 24 
D) 26 
E) 28 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 16: 
Establecer las letras que deben ir en reemplazo de X e Y en ese orden: 
A) I K 
B) I L 
C) J K 
D) J L 
E) J M 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 17: 
¿Cuál es la probabilidad que al tirar dos dados la suma resultante sea un cuadrado perfecto? 
A) 7/36 
B) 1/9 
C) 1/4 
D) 1/3 
E) 5/36 
RESOLUCIÓN :
Rpta. : "A"

PREGUNTA 18: 
A) 4 
B) 5 
C) 6 
D) 7 
E) 8 
RESOLUCIÓN :
Tema: Razonamiento deductivo 


Rpta. : "C"
PREGUNTA 19: 
En la siguiente figura, indique el símbolo que reemplaza al signo de interrogación. 

RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 20: 
Halle la figura que sigue a la sucesión. 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 21: 
Dados los cuadros siguientes: 
Entre las alternativas, indique cuál completaría el 4.º cuadro
RESOLUCIÓN :
En cada cuadro, el valor absoluto de las pendientes de los pares ordenados verticales es igual.
Rpta. : "E"
PREGUNTA 22: 
Dado el operador definido mediante: 
Halle el valor de x en la ecuación: 
(2 • x) • (x • 3) = (x • 1) • 4 
A) 0 
B) 1 
C) 2 
D) 3 
E) 4 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 23: 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 24: 
Un automóvil parte, de A rumbo a B, a las 12 del mediodía, con una velocidad constante de 36 km por hora; cuatro horas después, sale otro automóvil (en la misma ruta de A a B) con una velocidad de 40 km por hora, aumentando en 4 km su velocidad cada hora. ¿A qué hora alcanzará al primer automóvil? 
A) 8 p. m. 
B) 9 p. m. 
C) 10 p. m. 
D) 11 p. m. 
E) 12 medianoche 
RESOLUCIÓN :
Tema: Móviles 
Rpta. : "E"
PREGUNTA 25: 
 Definidos los operadores matemáticos por 
Determine el valor de x^m. 
A) 0 
B) 1 
C) 2 
D) 3 
E) 4 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 26: 
De 176 invitados a una conferencia, un cuarto se sirve solo café con azúcar, 5/8 lo toma con leche y azúcar, uno de cada 16 lo toma solo con leche y el resto no le agrega nada. Indique en este orden, ¿cuántos invitados consumen solo café? y ¿qué fracción representa de los que toman con leche? 
A) 11 ; 1/16
B) 11 ; 1/11
C) 11 ; 1/ 5
D) 55 ; 1/16
E) 55 ; 1/11 
RESOLUCIÓN :
Tema: Situaciones aritméticas 
Rpta. : "B"
PREGUNTA 27: 
Un granjero tiene solo gallos y gallinas, las cuales ponen un huevo cada día. Si cada día se recoge 96 huevos, ¿cuántas aves tiene el granjero? 
Información brindada: 
I. Por cada gallo hay dos gallinas. 
II. Por cada huevo hay 3 patas de aves. 
Para resolver el problema 
A) la información I es insuficiente. 
B) la información II es insuficiente. 
C) es necesario usar ambas informaciones. 
D) cada una de las informaciones, por separado, es suficiente. 
E) la información brindada es insuficiente. 
RESOLUCIÓN :
Tema: Suficiencia de datos 
De la información inicial tenemos que hay 96 gallinas:
De la información I: 
Por cada gallo hay dos gallinas, entonces hay 48 gallos. 
Luego, el granjero tiene 48 + 96 = 144 aves. 
De la información II: 
Por cada huevo hay 3 patas de aves, entonces por cada dos huevos hay 6 patas de aves, es decir 3 aves. 
Luego, como hay 96 huevos se tendrá 3×48 = 144 aves. 
∴ Cada una de las afirmaciones, por separado es suficiente. 
Rpta. : "D"
PREGUNTA 28: 
Juana tiene 3 amigos: Marcos, Luis y Víctor; que viven en tres ciudades distintas: Lima, Cusco e Iquitos, y tienen 3 carácteres distintos: tímido, liberal y agresivo. Se desea saber dónde vive Víctor y su respectivo carácter. 
Información brindada: 
I Marcos no está en Lima ni Luis en el Cusco, y el que vive en Iquitos es agresivo. 
II El que está en Lima no es tímido, en tanto que Luis no es liberal ni tímido. 
Para resolver el problema: 
A) La información I es suficiente. 
B) La información II es suficiente. 
C) Es necesario utilizar ambas informaciones. 
D) Cada información, por separado, es suficiente. 
E) Falta información. 
RESOLUCIÓN :
TEMA : Suficiencia de datos 
Tenemos: 
Ciudades: Lima; Cusco; Iquitos 
Nombres: Marcos; Luis; Víctor 
Caracteres: tímido; liberal; agresivo 
Piden: dónde vive Víctor y qué carácter tiene.
• Usando solo el dato I: 
► Marcos no está en Lima. 
► Luis no está en Cusco. 
► El de Iquitos es agresivo. Este dato no es suficiente. 
• Usando solo el dato II: 
► El que está en Lima no es tímido. 
► Luis no es liberal ni tímido. 
► Luis es agresivo y el de Lima es liberal. 
Esta información no es suficiente. 
Usando I y II se obtiene: 
Marcos    Luis    Víctor 
Cusco    Iquitos    Lima 
Tímido Agresivo Liberal 
∴ I y II son necesarias. 
: Es necesario utilizar ambas informaciones.
Rpta. : "C"
PREGUNTA 29: 
Se desea calcular la longitud del segmento MB de la figura si se dispone de las siguientes informaciones: 
I. MD(2BC+CA)=CA×DA 
II. BD(2BC+CA)=CA(CA – BD) 
Para resolver el problema 
A) la información I es insuficiente. 
B) la información II es insuficiente. 
C) es necesaria utilizar ambas informaciones. 
D) cualesquiera de las informaciones por separado es suficiente. 
E) las informaciones dadas son insuficientes. 
RESOLUCIÓN :
Tema: Suficiencia de datos 
Rpta. : "D"
PREGUNTA 30: 
Si yz ≠ 0, se pregunta si
Información brindada: 
I. x÷y <− 0,5
II. xy< 0 
Para resolver el problema: 
A) La información I es suficiente. 
B) La información II es suficiente. 
C) Es necesario utilizar ambas informaciones. 
D) Cada información, por separado, es suficiente. 
E) Falta información. 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 31:  
En una fábrica, la línea de producción A incrementa 5% del 2016 al 2017 y la producción en la línea B aumenta en 10%, en ese mismo periodo, ¿cuántas unidades se produjeron en 2016 por la línea A? 
Información brindada: 
I. Las dos líneas combinadas produjeron 100 000 unidades en 2016. 
II. Las dos líneas combinadas produjeron 107 500 unidades en 2017. 
Para resolver el problema 
A) La información l es suficiente. 
B) La información II es suficiente. 
C) Es necesario utilizar ambas informaciones. 
D) Cada información, por separado, es suficiente. 
E) Falta información. 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 32: 
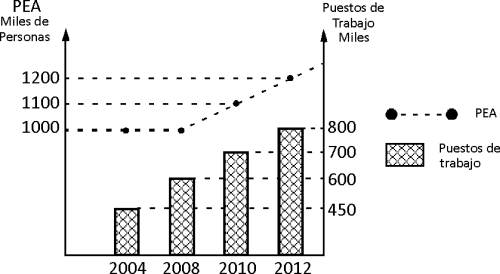
El gráfico muestra la estadística de los últimos años de la población económicamente activa (PEA) y de los puestos de trabajo. En base a la información, determine las afirmaciones correctas. 
I. La tasa de crecimiento de la PEA y de los puestos de trabajo, del 2008 al 2012 ha sido igual. 
II. La tasa de crecimiento de los puestos de trabajo ha sido mayor a la PEA en los últimos 8 años. 
III. El desempleo se reduce en los últimos 4 años. 
A) solo I 
B) solo II 
C) solo III 
D) I, II y III 
E) I y III 
RESOLUCIÓN :
Tema: Interpretación de gráficos estadísticos 
Rpta. : "B"
PREGUNTA 33: 
El gráfico muestra una figura que apareció en un diario de una ciudad. En él se indica la preferencia por el noticiero central de 5 canales de televisión según una muestra aleatoria en un año determinado. 
¿Cuál(es) de las siguientes afirmaciones es(son) verdadera(s)? 
I. De acuerdo a la muestra, el noticiero central con menor probabilidad de ser visto es TV5. 
II. El gráfico muestra exactamente la realidad de la preferencia de los noticieros de esta ciudad. 
III. Aproximadamente, un cuarto de la muestra no ve noticieros centrales de estos 5 canales. 
A) solo I 
B) solo II 
C) I y II 
D) I y III 
E) I, II y III
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 34: 
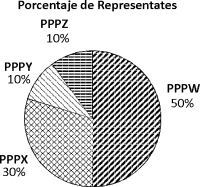
En el Congreso están elegidos 130 representantes que conforman 4 grupos con los porcentajes indicados en el gráfico circular. 
El día de una votación están ausentes algunos representantes como se muestra el cuadro. 
La votación obtenida después de un largo debate fue como se muestra en el gráfico de barras, en porcentaje referido al número de presentes. 
Todos los presentes votan, que representan el 100 % 
Con la información brindada, señale el valor de verdad (V) o falsedad (F) de las siguientes afirmaciones: 
I. De la agrupación PPPW ese día solo votaron 61 representantes. 
II. Si todos los miembros del grupo PPPW votó a favor, 27 miembros de otros grupos también votaron a favor. 
III. Todos los miembros presentes de la agrupación PPPZ votaron a favor. 
A) VVV 
B) VVF 
C) VFF 
D) FFF 
E) FFV 
RESOLUCIÓN :
Tema: Interpretación de gráficos estadísticos 
De acuerdo a la información consignada tenemos que el día de la votación estuvieron 61 representantes de PPPW, 36 representantes de PPPX, 11 representantes de PPPY y 10 representantes de PPPZ. 
Luego: 
I) La información es verdadera 
II) Como el total de votantes fue 120 y a favor fue 70% el cual es 84 votos, entonces 23 miembros de otros grupos también votaron a favor. La información es falsa. 
III) No hay evidencia que esto halla ocurrido, la información es falsa.
Rpta. : "C"
PREGUNTA 35: 
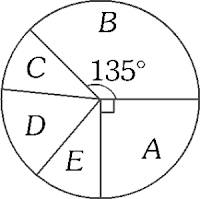
El gráfico adjunto muestra los resultados de una encuesta acerca de las preferencias del público respecto a los candidatos a la alcaldía de cierto distrito de Lima. Señale la alternativa correcta, después de determinar si la proposición es verdadera (V) o falsa (F). 
I. El candidato A tiene el 25 % de preferencia. 
II. El 37,5% de preferencia la tiene B. 
III. C, D y E suman igual porcentaje que B. 
A) VVV 
B) VVF 
C) VFV 
D) VFF 
E) FVV 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 1: 
Si: 
– Todos los pintores son artistas. 
– Ningún artista es deportista. 
Se concluye 
A) Algunos pintores son deportistas 
B) Ningún pintor es deportista 
C) Todos los artistas son pintores 
D) Algún deportista es pintor 
PREGUNTA 2: 
Alberto, Benito, César y Danilo tienen cada uno un boleto con los números 13, 16, 17 y 22, aunque no necesariamente en ese orden. Se sabe que: 
– La suma de los números de los boletos de Alberto y Benito, resulta primo; 
– La suma de los números de los boletos de Benito, César y Danilo, resulta par; y 
– La suma de los números de los boletos de Danilo y Alberto, resulta impar. 
¿Cuál es la suma de los números de los boletos de Benito y César? 
A) 35 
B) 29 
C) 23 
D) 39 
PREGUNTA 3: 
En una reunión se encuentran André, Boris, Cesar y Dino cuyas profesiones son médico, ingeniero, arquitecto y contador, aunque no necesariamente en ese orden. 
Se sabe que: 
– André no es amigo del ingeniero. 
– César es amigo del médico y del contador. 
– Boris no es arquitecto y no tiene amistad con César. 
¿Cuál de las siguientes afirmaciones son falsas? 
(I) André es ingeniero 
(II) Dino es arquitecto
 (III) César es arquitecto 
A) II y III 
B) I y II 
C) Solo I 
D) Solo II 

Tu academia preuniversitaria pdf para ingresar a la universidad practicando con preguntas resueltas de nivel básico intermedio y avanzado