RAZONAMIENTO MATEMÁTICO PRIMERA PRUEBA EXAMEN ADMISIÓN UNIVERSIDAD NACIONAL DE INGENIERÍA SOLUCIONARIO PDF

PREGUNTA 1 :

Si se tiene la siguiente sucesión:

– 8 ; 2 ; – 4 ; 4 ; 0 ; 6 ; X ; Y

Calcule el valor de X+Y.

A) 12

B) 14

C) 8

D) 15

E) 10

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 2 :

Halle y – x en

A) 0

B) –1

C) 5

D) 3

E) 1

RESOLUCIÓN :

Rpta. : "D"

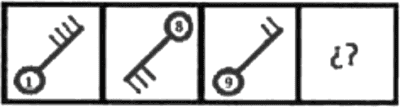
PREGUNTA 3 :

¿Qué figura continúa?

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 4 :

¿Cuántos cuadriláteros pueden contarse en la siguiente figura que contengan al menos una estrella negra?

A) 7

B) 6

C) 11

D) 10

E) 5

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 5 :

Halle Y/X en

A) 3

B) 4

C) 2

D) 5

E) 1

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 6 :

¿Qué figura continúa?

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 7 :

¿Qué figura es discordante?

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 8 :

Dados los operadores definidos mediante

A) 2

B) 6

C) 1

D) 7

E) 3

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 9 :

Dados dos operadores definidos mediante

A) 20

B) 0

C) –20

D) –42

E) –36

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 10 :

Dado el operador

A) 16

B) 2

C) 8

D) 32

E) 4

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 11 :

En cierto curso se desea conocer el promedio de cuatro notas de un alumno con la información brindada:

I. Sus últimas tres notas son iguales a 12.

II. Su promedio de notas sin tomar en cuenta la última es 11.

A) Solo es suficiente la segunda información.

B) Cada información por separado es suficiente.

C) Es necesaria ambas informaciones.

D) Falta información.

E) Solo es suficiente la primera información.

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 12 :

Sea el evento de extracción secuencial de bolillas sin reposición. Se desea conocer la probabilidad de sacar la cuarta bolilla de color rojo de una urna que contiene bolillas de cuatro colores: rojo, azul, negro y blanco cuyas cantidades son 3, 1 ,1 y 1 respectivamente, con la información brindada:

I. Se extrajeron dos bolillas de igual color.

II. Las tres primeras bolillas extraídas fueron de colores iguales.

A) Ambas informaciones son necesarias.

B) Solo la segunda información es necesaria.

C) Cada información por separado es suficiente.

D) Solo la primera información es necesaria.

E) Falta información.

RESOLUCIÓN :

Datos iniciales:

Hay 3 rojos, 1 azul, 1 negro y 1 blanco

DATO 1:

se extrajeron 2 bolillas de igual color

Casos: RRA RAR ARR RRN RNR NRR RRB RBR BRR

En todos los casos, para la cuarta extracción quedarían 1 roja y 2 esferas de otro color, y con esa información se podría calcular la probabilidad de obtener la bolilla roja (CF/CT = 1/3) ⇒ es suficiente.

DATO 2:

las tres primeras extraídas fueron iguales → RRR; de esta forma, para la cuarta extracción no quedarían esferas rojas y a eso le corresponde probabilidad = cero (aunque es 0 se ha podido determinar su valor) ⇒ es suficiente.

Rpta. : "C"

PREGUNTA 13 :

Estando en el año 2021, se desea conocer la edad actual de una persona que nació, al igual que sus hermanos, en años distintos del siglo XXI, con la información brindada:

I. Su edad es el producto de dos números primos gemelos.

II. Tiene dos hermanos, uno mayor y otro menor, cuyas edades son el producto de dos números primos impares.

A) Solo la segunda información es necesaria.

B) Solo la primera información es necesaria.

C) Cada información por separado es suficiente.

D) Ambas informaciones son necesarias.

E) Falta información.

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 14 :

Si al dividendo de una división se le agrega 48 unidades, el cociente y el residuo aumentan en tres unidades. El divisor es

A) 21

B) 18

C) 16

D) 15

E) 24

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 15 :

Sabiendo que (p ∨ q) ↔ (r ∧ s) ≡ V

y que r y s son proposiciones con valores de verdad opuestos, ¿cuál de las siguientes proposiciones son falsas?

a. r ∧ s

b. p ∨ q

c. ∼r ∨ ∼q

A) solo a

B) a y c

C) solo b

D) solo c

E) a y b

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 16 :

En las siguientes proposiciones y luego del respectivo análisis, determinar cuáles de las siguientes proposiciones son tautologías o no.

I. (p ∧ q) → [∼(∼p ∨ ∼q)]

II. (p → q) ↔ [∼(p ∧ ∼q)]

III. [((p ∨ q) → ∼r) ∧ (p ∧ q)] → ∼r

A) solo I

B) solo I y II

C) solo II y III

D) I, II, III

E) solo II

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 17 :

El rango de una lista de números es la diferencia entre el mayor número y el menor número de la lista. Por ejemplo, el rango de la lista 1, 5, 1, 6, 3 el rango es 6 – 1 = 5 ya que 6 es el mayor y 1 es el menor. Si la lista 11, 5, a, 13, 10 tiene como rango a 12, determine la suma de todos los valores que tiene a.

A) 21

B) 20

C) 16

D) 17

E) 18

RESOLUCIÓN :

Del enunciado , se define como rango a la diferencia entre el mayor y menor número de una lista de números.

Lista: 11; 5; a; 13; 10

Rango: 12

CASO 1: a es el menor número de la lista 13 – a=12 ⇒ a=1

CASO 2: a es el mayor número de la lista a – 5=12 ⇒ a=17

Por lo tanto, la suma de valores de a es 1 +17= 18

Rpta. : "E"

PREGUNTA 18 :

¿Cuánto le falta a la mitad de 2/3 para ser igual al cociente de 4/5 entre 2/3?

A) 1/2

B) 13/15

C) 7/9

D) 12/11

E) 1/5

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 19 :

Para un entero positivo se define el operador ∆(n) como el mayor exponente de la potencia de tres que divide a n.

Por ejemplo ∆(126) =3²×14 y por tanto ∆(126) = 2.

Si ∆(a) = 8; ∆(b) = 7, entonces hallar ∆(a+b).

A) 6

B) 7

C) 15

D) 12

E) 8

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 20 :

El gráfico muestra el número de casos confirmados de COVID-19 en el Perú durante el año 2020, estimando que la pandemia empezó en el mes de marzo. Señale la alternativa que presenta la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).

I. En la primera mitad considerada se tuvo el mayor número de infectados.

II. El número de meses en los que los casos disminuyó en relación al mes anterior en el año 2020 es 5.

III. Los casos en agosto representan el 25%, aproximadamente.

A) FVV

B) FVF

C) VFV

D) FFF

E) VFF

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 21 :

La siguiente tabla muestra el número de estudiantes de primero a cuarto año en la facultad de una Universidad y que juegan fútbol. Establezca cuál de los gráficos circulares muestra la información consignada en la tabla.

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 22 :

La siguiente gráfica muestra el número de postulantes (en cientos) a una universidad durante el periodo 2011 a 2021. En base a ello, señale la alternativa que presenta la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).

I. El porcentaje de disminución de postulantes del año 2019 al 2020 es del 37%, aproximadamente.

II. De acuerdo al gráfico solo hay dos periodos anuales cuando el número de postulantes ha aumentado.

III. El promedio de postulantes entre los años 2011 y 2015 es de 3960.

A) VVV

B) FVV

C) FVF

D) FFF

E) VFV

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 23 :

El gráfico muestra la temperatura promedio de dos ciudades en grados Fahrenheit a lo largo de un año. Señale la alternativa que presenta la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).

I. El número de meses en que la temperatura en la ciudad A ha sido mayor que en la ciudad B es 4.

II. El número de meses en que tanto la temperatura en la ciudad A y de ciudad B es por lo menos 60 °F es 6.

III. El menor temperatura de la ciudad A se dio en el mes de diciembre.

A) VFV

B) VFF

C) FVV

D) FVF

E) FFF

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 24 :

En este juego suponga que se tienen n platos que están igualmente espaciados en una mesa circular. Manuel desea ubicar un regalo en cada uno de k platos, de forma que los platos vecinos no tengan regalo. Definimos a f(n, k) como el número de formas en las cuales podemos colocar los regalos y por ejemplo f(6;3) = 2 como se muestra en la figura. Se pide determinar f(7;3).