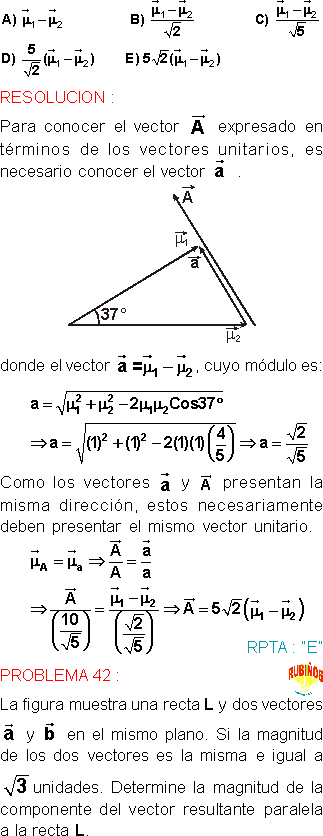VECTORES EJERCICIOS RESUELTOS CON EXPLICACIONES PASO PASO PDF
Para obtener mayor información de ciertos eventos es necesario indicar una dirección.
Por ejemplo, si 2 autos, en una pista, son igual de rápidos, podemos señalar una diferencia indicando hacia donde se dirigen, puesto que ; las direcciones de sus avances son distintas. Los vectores señalan una dirección.
VECTOR
Es un segmento de recta orientado (flecha), el cual nos permite representar geométricamente las magnitudes vectoriales.
Un vector se puede representar con cualquier letra del alfabeto, con una pequeña flecha en la parte superior.
MÓDULO DEL VECTOR
Es la medida, tamaño o magnitud del vector.
Está conformado por un valor numérico y su unidad de medida.
DIRECCIÓN DEL VECTOR
Está definida por la medida del ángulo obtenido a partir del eje horizontal positivo y la línea de acción del vector, medido en sentido antihorario.
- CLIC AQUÍ Ver VECTORES TEORÍA Y EJERCICIOS RESUELTOS PDF
- Ver VECTORES II RESUELTOS
- Ver VECTORES NIVEL BÁSICO
- Ver MÉTODO DEL PARALELOGRAMO
- Ver MÉTODO DEL POLÍGONO
- Ver MÉTODO DE LA DESCOMPOSICIÓN RECTANGULAR
- Ver VECTORES UNITARIOS
- Ver PRODUCTO DE VECTORES
- Ver PRODUCTO ESCALAR
- Ver PRODUCTO VECTORIAL
- Ver PROBLEMAS RESUELTOS UNI
Las nociones de vectores están implícitamente contenidas en las reglas de composición de las fuerzas y de las velocidades, conocidas hacia el fin de siglo XVII.
Es con relación a la representación geométrica de los números llamados imaginarios como las operaciones vectoriales se encuentran por primera vez implícitamente analizadas, sin que el concepto de vector esté aún claramente definido. Fue mucho más tarde y gracias al desarrollo de la geometría moderna y de la mecánica, cuando la noción de vector y de operaciones vectoriales se concretaron.
El alemán Grossman, en 1844, por métodos geométricos, introdujo formalmente las bases del cálculo vectorial (suma, producto escalar y vectorial).
El ingles Hamilton, por cálculos algebraicos llego a las mismas conclusiones que Grossman; empleó por primera vez los términos escalar y vectorial.
Hacia el final del siglo XIX, el empleo de los vectores se generalizo a toda la física. Bajo la influencia de los ingleses Hamilton, Stokes, Maxwell, Heaviside y del americano Gibas (quien utilizó la notación del punto para el producto escalar y del X para el producto vectorial) se amplió el cálculo vectorial, introduciendo nociones más complejas, como los operadores vectoriales gradiente, divergencia y rotacional.
PROBLEMA 1 :
Si el módulo de la suma de dos vectores de igual módulo es dos veces el módulo de la diferencia, el ángulo entre dichos vectores es
A) 15°
B) 30°
C) 45°
D) 53°
E) 74°
RESOLUCIÓN :
Rpta. : "D"
