5TO ACTIVIDAD 9 MATEMATICA EXPERIENCIA 2 APRENDO EN CASA QUINTO DE SECUNDARIA TAREA RETO WEB PDF

COMPRENDEMOS EL INTERÉS COMPUESTO EN SITUACIONES DE PRÉSTAMOS 
EXPERIENCIA DE APRENDIZAJE INTEGRADA 2 | 5.° grado ACTIVIDAD 9 
¡Hola! Como recordaremos en la actividad anterior, hemos reconocido y calculado interés simple en situaciones de préstamos. 
Ahora, con la finalidad de seguir construyendo nuestro aprendizaje, vamos a reconocer las características y uso del interés compuesto en situaciones de préstamos que se pudieran solicitar para iniciativas de emprendimientos.
¡Vamos a comenzar! 
Te presento la siguiente situación: 
Rafael, tiene en mente desarrollar una actividad productiva que le permita generar ingresos para la sostenibilidad de su familia. Pero, solo dispone de S/3000 de sus ahorros y le faltan S/3000 para completar lo que requiere. Por ello, acude a dos entidades con la intención de solicitar un préstamo. 
En estas entidades le proponen las siguientes opciones: 
ENTIDAD A 
ENTIDAD B 
Pago en cuotas mensuales durante 4 años. Tasa de interés compuesto de 20 % anual Pago en cuotas mensuales durante 4 años. Tasa de interés de 18 % a capitalización cuatrimestral. En base a la información respondemos: ¿Cuál sería la mejor opción para Rafael? Justifiquemos nuestra respuesta. 
TOMA EN CUENTA QUE 
Es importante que, en el proceso de resolución, primero comprendamos la situación, para ello, podemos responder: ¿qué datos se presentan en la situación?, ¿qué nos piden averiguar la situación? A continuación, después de leer la situación, respondemos las siguientes preguntas: 
a) ¿De qué trata la situación? 
b) ¿Cuánto dinero está pensando Rafael prestarse? 
c) ¿Cuál es la tasa de interés que ofrece cada una de las entidades? 
d) ¿En cuánto tiempo se cancelará el préstamo? 
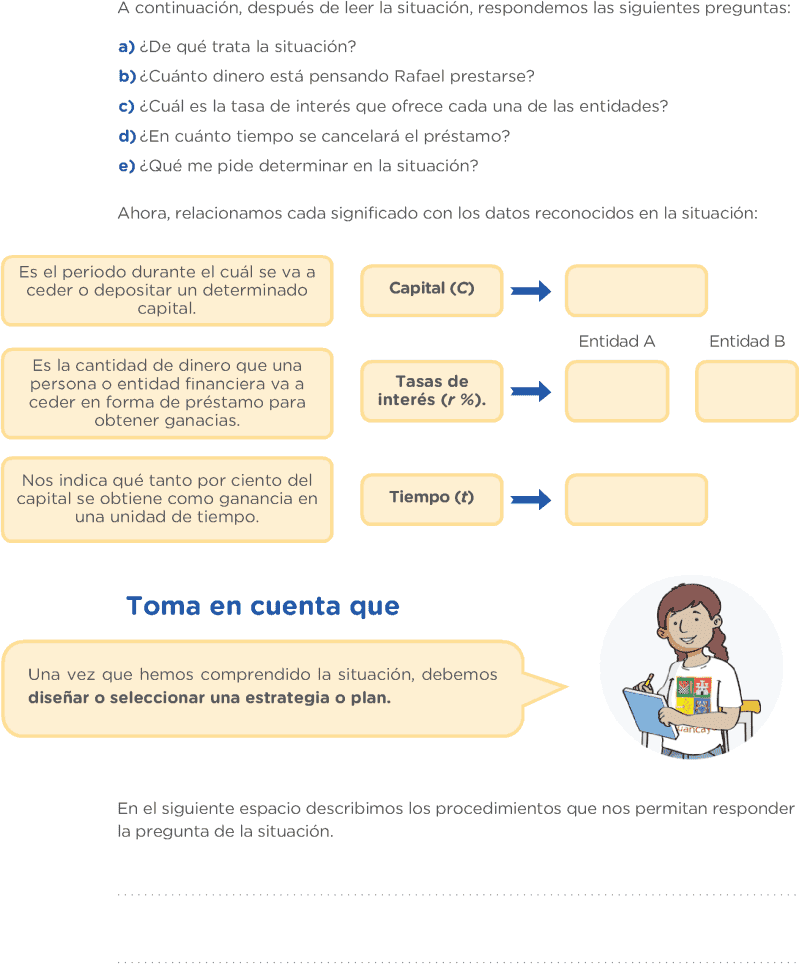
e) ¿Qué me pide determinar en la situación? Ahora, relacionamos cada significado con los datos reconocidos en la situación: Es el periodo durante el cuál se va a ceder o depositar un determinado capital. Es la cantidad de dinero que una persona o entidad financiera va a ceder en forma de préstamo para obtener ganacias. Capital (C) Tasas de interés (r %). 
Entidad A 
Entidad B 
Nos indica qué tanto por ciento del capital se obtiene como ganancia en una unidad de tiempo. Tiempo (t) Toma en cuenta que Una vez que hemos comprendido la situación, debemos diseñar o seleccionar una estrategia o plan. 
En el siguiente espacio describimos los procedimientos que nos permitan responder la pregunta de la situación. Ahora, es momento de ejecutar la estrategia o plan, para luego reflexionar sobre el desarrollo o el resultado obtenido. Leemos el texto “Interés compuesto” (página 1), el cual encontrarás en la sección “Recursos para mi aprendizaje”. 
En él se explica cómo calcular el interés compuesto de una cantidad. Para ejercitarnos un poco, realizamos las siguientes actividades: 
1) Calculamos el monto final y el interés que se generaría si Rafael solicita el préstamo en la “Entidad A”. 
a) ¿Cómo interpretamos la tasa de interés que cobrará la “Entidad A”? 
b) Después que hemos leído la información del anexo “Interés compuesto” (página 1), completemos la siguiente tabla con el interés y monto final que debe pagar a la “Entidad A” cada año. 
Recordemos expresar la tasa de interés como un número decimal. Año Capital (S/) Interés (S/) Monto final (S/) Año 1 4000 4000 (0,20) = 800 4000 + 800 = 4800 Año 2 4800 4800 (0,20) = 4800 + Año 3 Año 4 Respondemos las siguientes preguntas: c) ¿Cuál es el interés y el monto que se debe pagar después de un año? 
Justifiquemos nuestra respuesta. 
d) ¿Por qué el capital varía en el año 2; en 3 y en el 4? ¿Cuál es el monto final después de los cuatro años? 
a) Comprobamos el resultado del monto final sumando el capital del préstamo y el interés generado después de los cuatro años 
b) Calculamos el monto que tendría que pagar Rafael usando la expresión M = C(1 + r)t . Usemos la calculadora para realizar los cálculos. 
c) Comprobemos si la respuesta coincide en las actividades e y g. (Si no es así, revisamos nuestros procedimientos y corregimos). 
d) Calculamos el interés total generado en la “Entidad A” al terminar los cuatro años. 
2) Calculamos el monto final y el interés que se generaría si Rafael solicita el préstamo en “Entidad B”. a) ¿Qué significa que la tasa de interés se capitaliza cuatrimestralmente?, ¿qué diferencia tiene con la tasa que ofrece la “Entidad A”? 
b) ¿Cuántas veces al año se capitalizaría el monto, según la oferta de la “Entidad B”? 
c) Leemos el texto “Interés compuesto” (página 2), el cual encontrarás en la sección “Recursos para mi aprendizaje”. Luego, Calculamos el monto que tendría que pagar Rafael usando la expresión M = C 1 r t x n . Usamos la calculadora. ( + n ) d) Calculamos el interés generado por la “Entidad B” al terminar los cuatro años. 
Ahora reflexionemos y respondemos: ¿cuál fue la meta de aprendizaje que nos propusimos para esta actividad?, ¿qué acciones realizamos para lograrla?, ¿aprendimos a utilizar las expresiones para calcular un interés compuesto?, ¿en qué otras situaciones la usaríamos? 1) Una vez que obtuvimos los intereses y montos a pagar durante los cuatro años de cada una de las entidades, comparamos los resultados. Planteamos afirmaciones que nos permitan tomar decisiones sobre en qué entidad es conveniente o no para solicitar el préstamo, según la tasa de interés. 
¿Cuál sería la mejor opción para Rafael? Justifiquemos nuestra respuesta. 
EVALUAMOS NUESTROS AVANCES 
Ahora nos autoevaluamos para reconocer nuestros avances y lo que requerimos mejorar. Coloca una “x” de acuerdo con lo que consideres. Luego, escribe las acciones que tomarás para mejorar tu aprendizaje. 
Establecí relaciones entre datos y las transformé a modelos financieros de interés simple y compuesto. 
Además, verifiqué que el modelo financiero cumple con las condiciones del problema.
 Expresé con lenguaje numérico mi comprensión sobre las tasas de interés y los términos financieros (capital, monto y tiempo) para interpretar el problema en su contexto. 
Seleccioné y combiné estrategias de cálculo para resolver problemas sobre las tasas de interés, los evalué y opté por aquellos más idóneos, según las condiciones del problema. 

Planteé afirmaciones sobre la conveniencia o no de determinadas tasas de interés 
¡Muy bien, hemos culminado la actividad! 
En la siguiente actividad, vamos a resolver situaciones que involucran la comprensión de interés simple y compuesto que nos servirán para tomar decisiones sobre la conveniencia o no de determinadas tasas de interés para elegir un préstamo. 
Además, nos servirá de insumo para plantear afirmaciones sobre las tasas de interés en la cartilla. ¡Hasta la próxima actividad! 
INTERÉS COMPUESTO 
Se denomina interés compuesto a aquel que se va sumando al capital inicial y sobre el que se van generando nuevos intereses. Por ejemplo, si Manuela aceptara un préstamo de S/1000 a una tasa de interés del 10 % anual para pagar en 3 años, los intereses y el monto final se calcularían tal y como se muestra en la siguiente tabla: 
RECUERDA 
Cuando la tasa de interés se capitaliza en periodos de tiempo menores a un año, se debe calcular el número de veces que se capitaliza anualmente. Por ejemplo, si tienes un interés del 10 % capitalizable bimestralmente, entonces dicho monto se capitaliza 6 veces al año. 
COMPRENDEMOS EL INTERÉS COMPUESTO EN SITUACIONES DE PRÉSTAMOS

Tu academia preuniversitaria pdf para ingresar a la universidad practicando con preguntas resueltas de nivel básico intermedio y avanzado