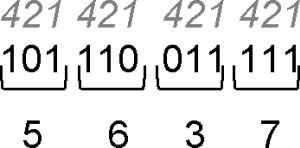EXAMEN ADMISIÓN CANTUTA 2023 SOLUCIONARIO UNIVERSIDAD NACIONAL DE EDUCACIÓN UNE PRUEBA DESARROLLADA PREGUNTAS RESUELTAS CLAVES RESPUESTAS PDF

RAZONAMIENTO MATEMÁTICO

PREGUNTA 26 :

Mañana será el ayer del antes de ayer del mañana del domingo. ¿Qué día fue antes de ayer?

A) lunes

B) martes

C) miércoles

D) jueves

E) viernes

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 27 :

La figura adjunta consta de 12 palitos de fósforo. ¿Cuántos de estos deben cambiar de lugar para que la figura tenga 7 cuadrados?

A) 1

B) 2

C) 3

D) 4

E) 5

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 28 :

En una conferencia hay 10 matemáticos y 15 biólogos; de los 10 matemáticos 5 también son biólogos, y de los 15 biólogos 5 también son matemáticos. ¿Cuántos tienen una sola profesión?

A) 30

B) 25

C) 20

D) 15

E) 10

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 29 :

Si la proposición ~ q → ~ t es falsa y la proposición p↔t es verdadera, entonces el valor de verdad de las proposiciones p, q y t, en ese orden, es

A) VFF

B) VFV

C) VVV

D) FFF

E) FVV

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 30 :

Dados los números p y q definidos como

p = 3/7 – 4/9

q = 11/5 – 4

es posible afirmar que

A) p es positivo y q es negativo.

B) p es negativo y q es positivo.

C) p es positivo y q es positivo.

D) p.q es negativo.

E) p.q es positivo.

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 31 :

Dadas las figuras, halle el valor de x

A) 5

B) 6

C) 7

D) 8

E) 9

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 32 :

Si definimos el operador *, entre los números reales, por *(a + b) = a + *(b), tal que *(3) = 5, entonces el valor de la expresión *(20) es:

A) 20

B) 21

C) 22

D) 23

E) 24

RESOLUCIÓN :

Utilizamos la regla del operador ∗ :

∗ (𝑎 + 𝑏) = 𝑎 + ∗ (𝑏)

∗ (3) = 5

Descomponemos: 20 = 17 + 3

Luego ∗ (20) = ∗ (17 + 3) = 17 +∗ (3)

= 17 + 5 = 22

Rpta. : "C"

PREGUNTA 33 :

Ruth tenía cierta cantidad de dinero y decide gastarlo. Gastó 3/7 en comprar un vestido, luego gastó las 3/5 partes del dinero restante en comprar un pantalón; por último gastó la mitad de lo que le queda en comprar una blusa. Si todavía le quedan S/40, ¿cuánto dinero tenía?

A) S/ 350

B) S/ 400

C) S/ 450

D) S/ 500

E) S/ 550

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 34 :

En la figura adjunta: si la medida del segmento AB es 8 cm y la medida del radio OM es 5 cm, entonces el área del rectángulo ABCD es

A) 40 cm²

B) 48 cm²

C) 56 cm²

D) 64 cm²

E) 72 cm²

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 35 :

En una reunión, a la que asisten 40 personas, el promedio de edades es 32 años. Si de dicha reunión se retira un grupo de 10 personas con un promedio de edad de 23 años, entonces podemos afirmar que el promedio de edad del grupo restante es

A) 28 años

B) 30 años

C) 35 años

D) 38 años

E) 40 años

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 36 :

Convierta el número 101110011111(2) a base octal (base ocho)

A) 5367(8)

B) 5673(8)

C) 5763(8)

D) 5637(8)

E) 6537(8)

RESOLUCIÓN :

La estrategia es separamos de derecha a izquierda, el número en base 2 y colocamos los números 1, 2 y 4 como se indica.

Luego se suman estos números en cada grupo solo cuando son unos. Así:

Rpta. : "D"

PREGUNTA 37 :

El valor de la expresión log 1 + log 100² + log 100 es

A) 3

B) 4

C) 6

D) 7

E) 9

RESOLUCIÓN :

Desarrollamos

log 1 = 0

log 100² = 2 log 100=2 log 10²=2×2log10=4(1)= 4

log 100 = 2

→ log 1 +log 100² + log 100 = 0 + 4 + 2 = 6

Rpta. : "C"

MATEMÁTICA

PREGUNTA 38 :

Sabiendo que los conjuntos

A= {𝑚² + 9 ; 𝑛 + 2}

𝐵 = {−9 ; 10}

son iguales calcule el valor de: (𝑚 + 𝑛)²

A) 10

B) 121

C) 49

D) 100

E) 1

RESOLUCIÓN :

Dos conjuntos son iguales, si tienen los mismos objetos (elementos).

En este caso m² + 9 no puede ser negativo; por lo que:

m² + 9 = 10 → m² = 1

También: n+ 2 = -9 → n= – 11

∴ (𝑚 + 𝑛)² = (1 + (−11))² = (−10)² = 100

Rpta. : "D"

PREGUNTA 39 :

Si el perímetro de un rectángulo es “𝑝” y la suma de los valores inversos de sus lados es 1/𝑠 , entonces ¿ cuánto mide su área en función de 𝑠 y 𝑝?

A) 𝑠 + 𝑝

B) 𝑠/𝑝

C) 𝑝𝑠

D) 𝑝/𝑠

E) 𝑝𝑠/2

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 40 :

Lucero repartió cierta cantidad de caramelos entre 3 niños en partes proporcionales a sus edades, que son 3, 5 y 8 años. Si el tercero recibió 78 más que el segundo, ¿cuántos caramelos repartió?

A) 412

B) 416

C) 244

D) 614

E) 420

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 41 :

Un poste tiene bajo tierra 2/7 de su longitud, 2/5 del resto sumergido en el agua, y la parte emergente mide 6m. Halle la longitud del poste.

A) 18 m

B) 13 m

C) 10 m

D) 14 m

E) 15 m

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 42 :

Si x es un número entero, tal que:

m = 3x + 1

n = x + 9

p = 2x + 3

Además, m> n>p.

Halle m + n + p

A) 42

B) 39

C) 43

D) 38

E) 45

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 43 :

De un grupo de 62 atletas de la UNE, 25 lanzan bala, 36 lanzan jabalina, 30 lanzan disco y 3 lanzan bala, jabalina y disco; además, 10 lanzan jabalina y disco, 15 disco y bala, 7 lanzan bala y jabalina.

¿Cuántos no lanzan jabalina ni disco?

A) 8

B) 6

C) 22

D) 7

E) 12

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 44 :

En un salón de clase de 65 alumnos se observó que:

– 30 son varones

– 40 estudian matemática

– Hay 10 señoritas que no estudian matemática

¿Cuántos son los varones que no estudian matemática?

A) 15

B) 20

C) 25

D) 14

E) 17

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 45 :

Si a y b son números enteros impares, entonces es(son) número(s) entero(s) par(es)

I. a – b

II. a.b

III. a.b – a

A) solo I

B) solo II

C) solo III

D) solo I y II

E) solo I y III

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 46 :

El cuadrado de la suma de dos números reales “x” e “y” disminuido en el cuádruple de su producto equivale al cuadrado de la diferencia de los mismos números.

Al representar la identidad anterior, se obtiene:

A) (𝑥 + 𝑦)² − 4𝑥𝑦 = (𝑥 − 𝑦)²

B) (𝑥² + 𝑦²) − 4𝑥𝑦 = (𝑥 − 𝑦)²

C) (𝑥 + 𝑦)² − 4𝑥𝑦 = 𝑥² − 𝑦²

D) (𝑥 + 𝑦)²+ 4𝑥𝑦 = (𝑥 − 𝑦)²

E) (𝑥 + 𝑦)² − 4𝑥𝑦 = (𝑥 + 𝑦)²

RESOLUCIÓN :

El cuadrado de la suma de dos números reales 𝑥 e 𝑦 : (𝑥 + 𝑦)²

Disminuido en el cuádruple de su producto: −4𝑥𝑦

Equivale al cuadrado de la diferencia de los mismos números: (𝑥 − 𝑦)²

Respuesta : (𝒙 + 𝒚)² − 𝟒𝒙𝒚 = (𝒙 − 𝒚)²

Rpta. : "A"

PREGUNTA 47 :

En la figura adjunta 0 es el centro de la semicircunferencia

Arco CB = Triple del Arco AC

¿Cuánto mide el ángulo x?

A) 22,5°

B) 30°

C) 45°

D) 67,5°

E) 75°

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 48 :

Con respecto a la gráfica de la función y = log x, es correcto afirmar que

A) corta al eje de las ordenadas.

B) corta al eje de las abscisas.

C) corta a todas las perpendiculares al eje de las X.

D) no corta a ninguno de los ejes coordenados.

E) corta a todas las circunferencias con centro en el origen

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 49 :

El valor de Sen37º. Csc37º – tg45º. Ctg45º es

A) – 1

B) 0

C) 1

D) 2

E) 1/2

RESOLUCIÓN :

Rpta. : "B"

¿Dónde solicito el Prospecto de Admisión?

El Prospecto de Admisión se entregará, previo recibo de pago, en cualquiera de las oficinas autorizadas

¿Hay doble opción en el Proceso de Admisión?

Sí. Las dos opciones pueden escogerse en una misma facultad.

¿Cuántas y cuáles son las facultades de la UNE?

Las UNE tiene siete facultades, y son:

1. Facultad de Agropecuaria y Nutrición

2. Facultad de Ciencias

3. Facultad de Ciencias Empresariales

4. Facultad de Ciencias Sociales y Humanidades

5. Facultad de Educación Inicial

6. Facultad de Pedagogía y Cultura Física

7. Facultad de Tecnología

EXAMEN ADMISIÓN CANTUTA 2023 SOLUCIONARIO UNIVERSIDAD NACIONAL DE EDUCACIÓN UNE PRUEBA DESARROLLADA PREGUNTAS RESUELTAS CLAVES RESPUESTAS PDF

Bruno montes